ダイクストラ法が分からなかった君のために
これはCompetitive Programming Advent Calendar 2015 の19日目の記事です。
さて、表題の通りこの記事はダイクストラ法についての思い出を語るものです。
競プロライフも2周年を迎え、取り組み始めたころに比べればかなりいろいろな問題も解けるようになりますます楽しくなってきたのですが、最初の頃割と長い間しっくりこないというか苦手意識のあったダイクストラ法について、振り返りながらいろいろ書いてみようと思います。
対象としてはダイクストラが分からなくてググるくらいの人も想定しています。ので多少くどい感じですがご容赦のほど。あともし大きな間違い等あればお知らせください。
ダイクストラ法とは
いきなりwikipediaを貼ってしまいましたが、グラフにおいてある頂点から別の頂点への最短距離を求める問題(単一始点最短経路問題)についてのアルゴリズムのうちの一つです。例えば下の絵のような状況を考えます。
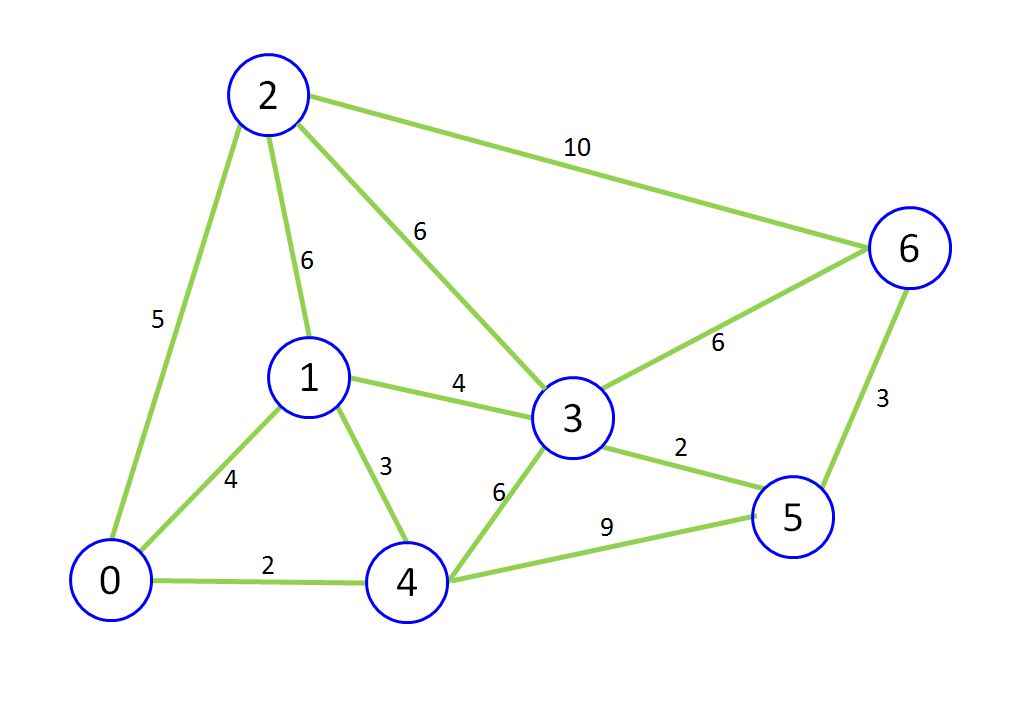
青丸を「頂点」、緑線を「辺」と呼びます。絵から想像できるように、ある頂点から別の頂点には辺を通ってのみ移動できるという状況です(あるいは、移動できる頂点間に辺が張られている)。各辺に付随している数を「コスト」とよび、この辺を移動するのに必要なコストを表しています。単一始点最短経路問題は、ある頂点から別の頂点への移動手段のうち、もっともコストの低い経路(のコスト)を探す問題です。
例えば、頂点を都市、辺を交易路、コストを交易路の距離とすれば、都市0から都市6へ行くにはどの交易路を選んでいけば最短距離でたどり着くことが出来るか、という問題になります。あるいは、頂点を駅、辺を路線、コストを運賃だと思えば、駅0から駅3へは最低いくら必要か、という問題にもなります。古典的問題のため、そのままコンテストで出題されることもさることながら、何を頂点、辺、コストと見立てるかによって応用範囲が広く、いろいろなケースで出題されることのある題材です。以下では頂点の個数を\( V \)、辺の本数を\( E \)で表します。
そもそも、どうやって求めるべきなのか
とりあえず最初に考えるのは、とにかく全ての経路をたどってみて一番短いものを選ぶという事です。

頂点0から頂点6に向かう経路は、同じ頂点を2回通らないという決まりだけで列挙すると40通りあるようです。これがでも次のようなグラフだとどうでしょうか。

コストを省略していますが、どの頂点からどの頂点にも辺が張ってある場合です。この時、頂点0から頂点6に向かう経路は(同じ頂点を2回踏まない制約があっても)326通りあります。一般に頂点が\(V \)個あるとすると、このように全ての頂点間に辺が張ってある場合は同じ頂点を2回踏まない制約でも \( \sum k ! (k=1,2,\dots,V-2) \) 通りの経路が存在します。これは莫大な量で例えば\( V=100 \)程度でも\( 10^{153} \)程度の数になります。ピンとこないくらい大きな数字です。よく言われる目安として現在のCPUは1秒間に大体1億回( \( 10^8 \)回)の計算ができると言うところから考えるとヤバさが分かると思います。1年かけても高々31536000秒です。
計算量のオーダーでいうと、\( O(V!) \) 程度になります。階乗はマズイやつですよ。。
最初の例に戻ると、仮に最短経路長が13だと分かっていれば、例えば経路探索の途中で15や16に既に達している場合はその先に進む理由がないので、その部分は枝刈りすることが出来ます。しかし、最短経路やそれに近い少しだけ遠回りが複数あるような場合は、ギリギリまで最短経路長を更新するかどうかわからず、結局上のように膨大なルートを検索しなければいけません。困った。
動的計画法のこころ ~これ、単一始点最短経路"長"問題じゃね?~
最初の例をもう少しよく眺めてみます。最短経路はどうやら2つあり、
- 0 ⇒ 1 ⇒ 3 ⇒ 5 ⇒ 6
+4 +4 +2 +3 - 0 ⇒ 4 ⇒ 3 ⇒ 5 ⇒ 6
+2 +6 +2 +3
となっているようです。さて、頂点3まで到達してしまうとあとは頂点5、頂点6とたどるしかないのですが、頂点0から頂点3にコスト8 で到達する道のりが2つあるために、頂点0から頂点6への最短経路自体の個数も増えているようです。
ここで動的計画法のこころが降りてきます。頂点3に辿り着くとそこから頂点5⇒頂点6と進むのが最短であるならば、頂点0から頂点3に辿り着くすべてのコスト8の経路はもれなく頂点0から頂点6への最短経路の一部になります。このことを考えると、経路そのものが大切なのではなく、どの頂点にいくらのコストでたどり着けるのかが大切であることに(天啓によって)気づきます。あるいは、ある頂点に対してあるコストで到達できる経路全体を同一視して、(頂点,コスト) という組に代表させると言い換えてもいいかもしれません。
そうだとすると、各頂点に対して次のような星取表を作って埋めることを考えてみます。(これはいわゆる配るDPと呼ばれるものです)

横軸に頂点番号、縦軸にコストを取り、もしそのコストでその頂点に到達できることが出来るならそのマスを塗っていきます。スタート地点には必ず立てるので、コスト0で到達していると考えます。さて、頂点0からは
- コスト4で頂点1へ移動できる
- コスト5で頂点2へ移動できる
- コスト2で頂点4へ移動できる
ので、それぞれ移動できるところに色を塗りましょう。

このような操作
- 「ある頂点にコスト \( k \) で到達できるならば、その頂点から辺が出ている頂点に、コスト ( \( k + \) その辺のコスト) で到達することが出来る(ので色を塗る)」
を"配る"と呼ぶことにします。今回の例では、辺のコストは全て0より大きいので、配り続けていくと塗られるマスはどんどん上に向かって伸びていきます。なので、下からローラー作戦で配って行けば、塗りもらしなく星取表を埋めていくことが出来そうです。やってみましょう。

こうやって表にしてみると、例えば頂点1に辿り着くことのできるコスト(の集合)は\( \{4,5,8,9, \dots \} \)という事が分かります。頂点1に辿り着く最短コストはこれらの中の最小値なので4、という事になります。同様に、確かに頂点6に辿り着く最小コストは13になっています。
回りくどいように見えますが、実は計算量と言う点ではこの時点でかなり効率化されています。縦方向にどこまで配り続ける必要があるかと言う点は現時点では不明なので、これを\( D \)と置きます。横方向に1回走査すると、各頂点からすべての辺が1回ずつ登場しているので、計算量は\( O(E) \)となり、縦方向は\( D \)回配るとすると計算量は\( O(D \times E) \)になります。
\( D \)の上界ですが、例えば各辺のコストが高々\( K \)くらいだとすると、辺全部を足しても\( K \times E \) なので\( D=K \times E \)くらいに取っておけば絶対大丈夫でしょう。すると\( O(D \times E) = O(K \times E^2) \)くらいです。\( E \)はせいぜい\( V \times V \)なので、大体\( O(K\ \times V^4) \)くらいの計算量になります。\( V=100 \)で経路を数え上げると\( 10^{153} \)くらい必要だった計算量は\( K \times 10^8 \) くらいまで減る見積もりになります。大体\( K \)秒くらいで終わりそう。だいぶ絶望感がなくなってきた?
効率よく次を探す ~ダイクストラ法その1、その2~
上の方法でやっていけば現実的な時間で終わりそうですが、いくつか課題があります。
- 辺のコストが大きいとそれだけ時間がかかる
- 辺のコストが整数でないと使えない
\(D\)が扱う辺のコストに左右されて不当に大きくなることで全体の計算時間が増えるのはいただけない。また、コストが整数でないと使えないというのは、例えば小数なら全体に10の何乗かを掛けて整数にしてしまうと言う手もあるかもしれませんが、\( D \)がやはり大きくなってしまったり、また例えばXY平面上の距離のような無理数だと大変苦しい。
そこでもう一度上の図をグッと睨んでみると、いろいろと非効率な部分が見えてきます。そこをもう少し効率化することを考えましょう。
コストの低い方から順番に配ることによって、各頂点に対してその頂点に到達することのできる経路コストの候補がどんどん列挙されていきますが、列挙されたコストのうち最小のものが決定するタイミングはいつになるか、と言う視点で上の星取表を眺めていると、各頂点に対して最初に配る側の立場に立ったマスが最小コストを表していることが分かります。例えば下の図において、(頂点3,コスト8)というマスは、(頂点4,コスト2)というマスから配られて色を塗られますが、頂点3への最小コストが8だと決定するのはあくまで(頂点3,コスト8)というマスが配る側の立場に立った時です。


つまり、下から順に見て行って、「初めて配るマス」を順に決めて行けば効率よく最短コストを確定させながら表を埋めていけそうです。「初めて配る」立場に立つ、というのは言い換えればもうそれより手前のマスから配られることは無い、ということなので、ある頂点から配り終わった後、配られたマスのうち、まだ配ったことのない頂点の中から一番手前にあるものを選べばよいということが分かります。

ダイクストラ法が行っているのはこの操作になります。この方法であれば縦方向の \( D \)が整数でなくても良いし、どんなに大きな数でもそれで計算量が変わることはありません。ただし、次の候補が上にあることが前提で探すため、負コストの辺があるときはうまくいきません。
ダイクストラ法(その1) 横方向に探す
既に配られたマスの中で、まだ配ったことのない頂点の中から一番手前にあるマスを探す、という処理をすなおに考えると、\( V \) 個の頂点を一つ一つ確認してまだ配ったことのない頂点の中から最小の到達コスト候補を持つ頂点を選べばいいです。表でいえば横方向、頂点ベースで探すということになります。これがいわゆるオリジナルのダイクストラ法の方法です。
下の図では、既に配り終えた(最短コストが確定した)マスはFixに○が付いています。Fixしていない頂点から一番小さいコストを探して、ピンクのはこで囲っています。

計算量は、 \( V \)個の頂点をチェックするという処理を \( V \)回行うため、この操作だけで \( O(V^2) \) のオーダーになります。配る操作が各頂点ごとに発生するのですが、各頂点から各辺は1回だけしか配られないことを考えると、配る操作のトータル計算量は \( O(E) \) 、アルゴリズム全体では \(O(E+V^2) \) になりますが、\( E \) は高々 \( V \times (V-1) /2 \) なので \(O(V^2) \) となります。また、実際にプログラムに書く際にはこのような表をつくる必要はなく、最小コスト候補だけを覚えておけば事足ります。
ダイクストラ法(その2) 縦方向に探す
同じように、次に配る頂点を今度は縦方向、コストに着目して探す方法を考えましょう。要はいままでに配られたマスの中で一番手前にあるマスを選べばいいのですが、例えば既に \( V_0 ( \leqq V ) \) の頂点から配られているとすると、最大 \( {V_0}^2 \) 個くらいのマスが候補にあるため、それらから単純に一番手前のマスを選ぶというのは場合によっては \( V \)個の頂点を確認するより時間がかかりそうです。そこで優先度付キューを使います。優先度付キューは、\( N \) 個のキューに掘り込まれたものの中から一番小さいものを \( O(log( N )) \)の計算量で取り出すことが出来るキューです。これを使えば今までに配られたマスのうち、まだ配ったことのない頂点を探すことが効率的に行えます。(取り出したマスがまだ配ったことのない頂点なら採用して配る、すでに配ったことのある頂点なら捨てる)
下の図では、ピンクの箱が優先度付キューから取り出されたマスを、赤の箱が優先度付キューに追加された(エンキュー状態の)マスを表しています。

計算量を考えるにあたって、ここではオーソドックスな優先度付キューを採用することにして、キューの保証する性能として\( N \) 個追加されている状態からの要素の取り出し、要素の追加にそれぞれ \(O(log(N)) \)かかるものとします。
まず配る操作が各頂点ごとに発生するのですが、配る操作は優先度付キューへの追加に相当します。一番最悪な状況を考えると、最後の頂点の候補を取り出す時にそれまでの全ての辺を通じて配られたマスがごみとしてキューに残っている状況が考えられるため、キューへの追加に\( O(log(E)) \)かかると見積もっておけばよさそうです。配られるマスの数は各辺が1回だけなので最大\( E \) と考えると、配る計算量のトータルが\( O(Elog(E)) \)になります。
あとは取り出す動作ですが、これも最低 \( V \)回は取り出さなければならないことを考えると、\( O( V log(E) ) \)は必要ということになります。ただ、確定済みの頂点もキューに放り込まれていることを考えると、pop(取り出し)の回数は厳密には \( V \)より多くなると考えられます。これを\( V^{*} \)と書くことにして、\( E \) で抑えられると思っておきます。
2つの合計として計算量は \( O(E log (E) + V^{*} log(E)) \)となります。\( V^* \leqq E \)と\( log(E) \leqq 2 log (V) \)で抑えたとすると \( O(Elog (V)) \)が保障されると考えていいでしょう。
その2の方法の良く知られた高速化として、最小コストが更新される可能性のある場合だけキューに追加するというものがあります。これはキューにたまるゴミが減ることがもたらす効果になります。
(その2の方法の小手先の高速化として、全頂点確定したらwhileのループから抜けるというのがあります。優先度付キューをpopで空っぽにするのは意外と時間かかるよ!)

あと、さらに縦方向にさがすキューを高速化した特別なケースとして、縦軸が非負整数の場合にyosupoさんのスライドで紹介されているRadix Heapの方法があります。
(あと余談ですが、C#には優先度付キューが標準ライブラリにないので自作せねばならず、いまから未知のアルゴリズムを勉強するのにライブラリも作らなあかん、というのがいくらか障壁になっていたことも書いておきます。そういうやつは逆に道具をそろえるとやる気になるので、ピンチはチャンスの精神で)
効率よく表を埋める ~ベルマンフォード法・SPFA~
最初の表に戻ってもう一度考えてみると、他の単一始点最短距離"長"問題のアルゴリズムについても同じようにこの表を効率的に埋めているのだと考えることが出来ます。
ベルマンフォード法 ~そんなD回もまわさんでええんやで~
配るDPでとりあえず距離\( D \)を上限にして1から回していきましたが、実は頂点数 \( V \)に対して、 \( V-1 \)回回せば十分と言うことが、やはり表の動きをグッと睨んでいると分かります。
現在自分がある頂点にいたとして、1回表を横に走査するという操作は、その頂点から1歩動くことを意味します(当たり前)。なので、最短経路を探すに当たり同じ頂点を2度訪れることはありえないことを考えると、最大\( V-1 \) 歩しか進まないはずで、逆に最短経路が\( N ( \leqq (V-1) ) \)歩で達成できるとすると、上のDPローラーが始点含めそれより前の \( N \)点の頂点と到達コストのそれぞれを踏みさえすればいいことが分かります。

「そんな都合よくローラー走査すべき行がみつかるかいな」と思うかもしれませんが、実はこの表の特定の行を走査する必要はありません。配る頂点で本当に必要なのは、最小コストの頂点だけです。なので、毎回のローラー走査では最小候補となるマスからだけ配っておけばよいです。
下の図では、最小コストの頂点から配っていく様を表しています。緑色の線が、最小値を更新するポイントを表します。

(頂点のナンバリングが悪くて、ローラーの横方向を昇順に走査すると1順で全ての最短路が列挙されてしまいました。下は同じグラフで降順に走査した場合です)

計算量は、最大 \( V-1 \)回の操作を必要する場合があることから \( O( (V-1) E) = O(VE) \)になります。ただ、上の図を見て分かるように、ローラー走査する回数は最短経路を実現する歩数の最大値なので、場合によっては途中から同じ動きの繰り返しになります。なので実装ではローラー走査一回ごとに前回との差分が生まれているかをチェックして、更新が無ければその時点で打ち切るのが一般的です。ダイクストラには劣りますが、辺の値とコストしか見ていないため負辺があっても"正しく"動作するため、負閉路検出等への応用があります(すみませんここ勉強不足なのでまたどこかで・・・)
SPFA ~もうちょっと効率化してみる~
基本的にベルマンフォード法の方式で上の表を埋めるにあたって、別にすべての辺を走査する必要はないよねというのがSPFAの動作になります。一回配る立場に立った頂点からは、その最短コストが次に更新されるまでは配る必要がないはずです。
配られていない頂点はまだ配ることができないので、配られた頂点だけが対象になるのでこれをキューに入れて管理します。また、各頂点の最小コストだけ分かっていればいいので、それは別で管理しておきます。ダイクストラの場合は、「頂点とコストの組」を優先度付キューに入れておかなければ意図した頂点が見つからないため、キューの外で管理することはできませんが、SPFAの場合はとにかく配れれば良いのでキューには頂点だけを入れればよいです。言い換えれば、「頂点とコストの組」をキューしたつもりになっておいて、その頂点がキューから取り出される前に最小コストが更新された時は、キューされた「頂点とコストの組」のコストが書き換わったと考えればいいということでもあります。そのため、エンキュー状態にあるかというフラグも各頂点で持っておきます。
このようにしておけば、ベルマンフォード法においてもう配る必要がなくなった頂点が除外される分だけ効率的になることが分かります。ただ、例えば\( n \)歩で見つかった最短経路長候補が \( m ( > n ) \)で更新された時に、既にキューからその頂点が取り出されていた場合は再度エンキューされるため、ダイクストラ法のように最初にキューから出てきたときに最小コストが保障されるわけではないことに注意が必要です。
分かりにくいですが、赤い箱がエンキューを表しています。エンキューされた状態で最小コストが更新された場合も同じように赤い箱で囲んでいますが、キューの中身は変わっていません。また、頂点6に着目すると、コスト14のところからと、コスト13のところと2回配っているのが分かると思います。

計算量ですが、ベルマンフォード方式よりは速そうだけど、言っても枝刈りなのと、いかにも\( O(VE) \)のオーダーでないと計算できない例が作れそうなので、最悪\( O(VE) \)という気がします。ここによるとランダムケースでは\(O(E)\)のオーダーらしいです。うーんこれはちゃんと証明見ないと分からないなすみません。
あの、結局僕はどういう経路を通ればいいのでしょうか(哲学) ~経路復元~
単一始点最短経路"長"問題じゃね?と思い直してから、効率的に最小コストを求めることが出来るようになりましたが、じゃあ実際どういうルートをたどればそれが実現できるのよ?という問いがまだ残っていました。しかし最初に述べたように最短経路自体は、なんの制約もなければ山のようにある可能性があります。どうしたものか。
実は、どのアルゴリズムを使っても、全頂点に対して始点からの最小コストが求まっていることに気づきます。これをうまく利用することで、一歩一歩が確実に最短経路から外れずに目的地に向かっているかを判定することができます。ポイントはゴールから逆算するというところ。ゴールを始点にして、各頂点への最小コストを求めておきます。以下のように判定しながらゴールを目指せばいいです。
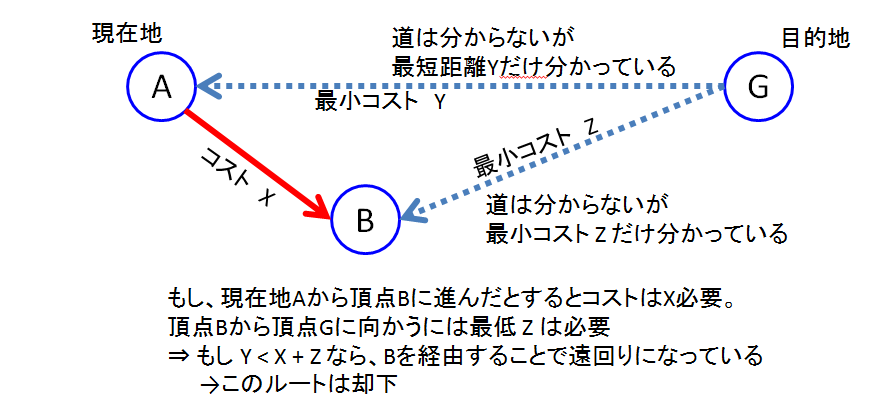
最悪計算量として\(O(E) \) くらいで見つかります。人生もゴールからの逆算で今のふるまいを決めていければいいのにねとおもわないでもないが、最小コストで行けばいいというものでもない。
で、どれがいいのよ? ~ベンチマークしてみる~
さて、これら4つのパフォーマンスについて、せっかくなのでベンチマークしてみました。
表中の系列はそれぞれ
- Dijk1 \( O(V^2) \) ダイクストラ,
- Dijk2 \( O((E+V)logE) \) ダイクストラ
- Dijk2 \( O((E+V)logE) \) ダイクストラ・枝刈りあり
- Berm \( O(VE) \) ベルマンフォード
- SPFA \( O(VE) \) SPFA
で、各グラフの
上段は横軸が頂点数 \( V, ( 10 \leqq V < 4000 ) \) 、
下段は横軸が辺の数 \( E, ( V \leqq E < V*(V-1)/2 ) \)
で縦軸がそれぞれ計算に要した時間[msec]になります。


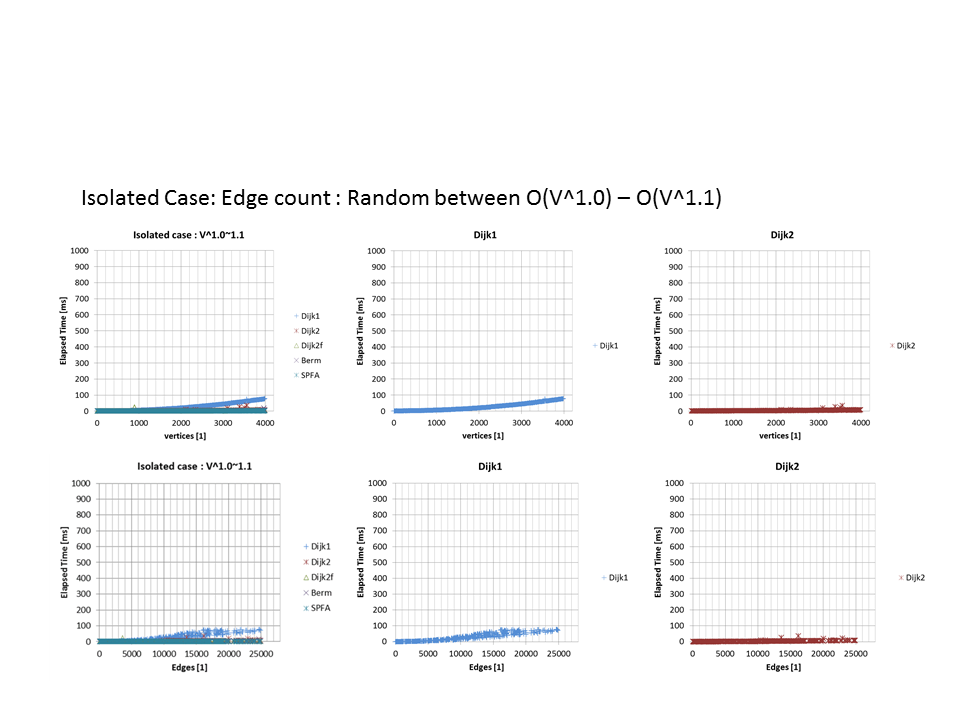
うーん、これだけ見ると枝刈りダイクストラ一択って感じだけど、ベルマンフォードとSPFAが思ったより速いのが結構意外という気がします。適当なランダムケースだからかなぁ・・・あと確かに \( O(E) \)っぽくなってる。
枝刈りしない優先度付キューはヤバい。枝刈りしよう。
以下、辺の密度ごとのプロットも載せておきます。確かに疎なケースでは \( V \) 成分が \( O(V^2) \) ダイクストラだけ見えていたりしてなかなか面白い。


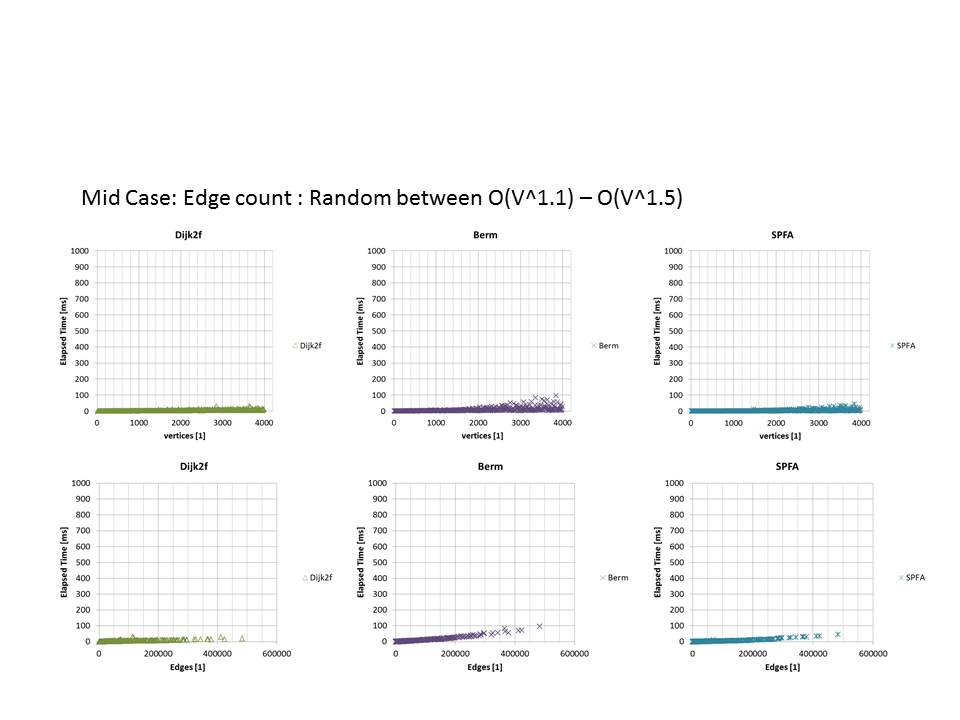


一応ソースコードのリンクを載せておきます。適当なC#なので読めればいい人向け。。
CPAC 2015のベンチマーク用ソースコード · GitHub
参考にしたページや問題など
参考:
2011/12/19 - Leftist Heap & Skew Heap
ダイクストラやってみたい方向け
Programming Problems and Competitions :: HackerRank 延々ダイクストラやる
No.160 最短経路のうち辞書順最小 - yukicoder 経路復元
Winter Bells | Aizu Online Judge 経路復元+数え上げ
おわりに
単一始点最短距離問題の代表的アルゴリズムであるダイクストラ法について、理解に至るまでいろいろ考えたことを振り返りながらまとめてみました。
競技プログラミングをやっていく中で多分多くの方が動的計画法につまづくと思い、最初は同じ題材で「古典的アルゴリズムに学ぶ動的計画法のこころ」という記事を書こうとしていたのですが、いつの間にかタイトルが変わり中身も変わってしまいました。とはいえ、かなりの紙面を配るDPに割いたので、なにかつまづいている人の理解の一助にでもなれば望外の喜びです。たとえばDPの表の縦軸をbitで管理した訪問済み/未訪問の値にして色を塗っていけば巡回セールスマン問題になったり、色を塗るというboolの部分を最小コストに置き換えて行ったり。いろいろとバリエーションはあるものの、「上手く問題を置き換えてまずローラー作戦する土壌を考える→重複や要らない情報を削ったり、データ構造をうまく使って計算を高速化する」という流れは、DP問題を解く王道パターンなので。
と、思っていたのに途中からアルゴリズム比較の方が面白くなってきてこんな記事になったという次第です。
ではでは。
明日(まぁ、記事公開は間に合っていないのですが・・・)の担当はHiroyuki Sanoさん(CPACその1)とMさん(CPACその2)です。お楽しみに!