2018の競プロ反省と記憶に残るバグたち

2018年も終わるので，今年の反省など．

戦績

AtCoder

1853 -> 1823（season Highest 1949)

伸び悩み中．黄色になれないことは無いとは思うけど現実は無情である．

CodeForces

1870 -> 1918 (season Highest 1962)

今年は結構参加してた．Highestは更新してないけど紫にはちょくちょく戻ってた印象

TopCoder SRM

1365 -> 1464 (season Highest 1555)

今年は参加数が減ってる．Highestは更新してない．

TopCoder MM

1348 -> 1223 (season Highest 1408)

今年は頻繁に開催されてる割に5回しか出てなかった．時間とMP/HPが確保できなかったね．

2018にやってみていたこと

2017年の後半くらいから伸び悩み自体は感じていたので，今年はいろいろやってみようとは思ってました．

ACアカウントを作る．

コンテスト中やコンテスト後に解いた問題数を把握するのに，twitterでAC垢 @kuuso1ac を作って1月からつけてました．アイコンが本家よりかわいいの気に入っています． 効果があったかはわからないですが，反省用にあとから集計すると意外と面白かったので来年以降も続けようかな．

トータルで552問解いたようで，数字だけで言えば多くはないが少なくもないよねと言ったところ．簡単な問題も入ってるので次のレベルに上がるには質が足りてないという事かなという気はする．

過去問埋め

上のグラフから見えるように，AtCoderの過去問埋めをやってました．500以上を埋めるのと1月からはStreakキープにもトライ．実際には4月から異動でリアルの方に余裕がなくStreakは105で途切れ，500点以降の問題を中心に進める方についてはいったん500,600は埋めて700があと1/3程度，最近はまたちょっと忙しかったので十分には進められていないですね．もうちょっと何とかしたい．

あと一時twitterのTLで流行？した「いいねの数だけACする」というのもやってみていて（これ），これもまぁまぁ，解いただけツリーにぶら下がっていくのを見る楽しみはあると言えばありますね．ところで進捗どうですか？

反省は？

いろいろあるような気もしますが，伸び悩んでいるときに出るのはおおむね負の感情なので今年は結構つらかったなというのが正直なところ． 自分の思っている理想のラインと現実のギャップが埋まらないというのは往々にしてよくある話だし，それを埋めるためにはどうももうちょっと何かブレイクスルーが要るのかなぁと思ったりもする．がアイデアが「時間と量で殴る」ぐらいしか思いつかなくて，それも確保するのに難があって，行き詰っている感がありますね．MMなんかはそもそも時間確保できずしぬを繰り返しただけの感がある．

今年は上にも書いたように異動があって環境が落ち着かなかったというのももちろんあるとは思ってるんですがそれはさておき，競プロももう5年目だし実力が収束してくるのは仕方ないにしても，愉しみがレートにしか依存しない状況が続くと本来面白いからやっていたはずの趣味が苦痛でしかなくなってくるので，違う楽しみ方をみつけないとなという点が大きな課題．学生のようにICPCやJOI/IOIといった期限付きではないという点は社会人競プロの強みであり弱みであると思うので，特にその強みを生かす方向で解があるだろうとは思う．どうしてもつらいならやめればいいはずだし，他に趣味をみつけるのもいいはず．

（それらを見つけることを大きく阻害している原因の一つに，後から始めた人々に追い抜かれていくのがいまだに辛いという本質的なメンタルバグがあり，どうしても目の前のレートに喜怒哀楽がひきずられている）

話を変えて

あまりネガティブになってもしょうがないので，今年みつけた印象的なバグを4つほど紹介します．ほかの方の参考になる記事が書ければ，今年にも意味があったという気分になるね！

1. UnionFindでStack-overflowする話

まずはコード．C#です．

using System;
using System.Collections;
using System.Collections.Generic;
using System.Linq;
using System.Text;

class TEST{
    static void Main(){
        Sol mySol =new Sol();
        mySol.Solve();
    }
}

class Sol{
    public void Solve(){
        int N = (int) 3e5;
        var UF = new UnionFind(N);  // Nノードの Union Find のインスタンスを生成
        for(int i=0;i<N-1;i++){
            UF.Unite(i, i+1);    // 隣同士を連結していった
        }
        Console.WriteLine(UF.IsUnited(0, N-1)); // ここでRunTimeError
    }
}

class UnionFind{
    
    int[] parent;
    int N;
    public UnionFind(int n_){
        Initialize(n_);
    }
    
    public void Initialize(int n_){
        N = n_;
        parent = new int[N];
        for(int i=0;i<N;i++){
            parent[i] = i;
        }
    }
    
    public int Parent(int a){
        if(parent[a] == a) return a;
        return parent[a] = Parent(parent[a]);
    }
    
    public bool IsUnited(int a,int b){
        return Parent(a) == Parent(b);
    }
    
    public void Unite(int a,int b){
        a = Parent(a); b = Parent(b);
        if(a == b) return;
        parent[a] = b;
    }
    
}

RankをつかわないUnion Find（これとか）を使っていますが，上のようなシチュエーションでStack-overflowしましたね．今までもありそうなケースだったけど，Rankをつかっていないため再帰深度がO(N)になっていた．

みんなもRankを実装しましょう．（これ確かFHCかGCJだったかでローカルテストしていたので，その時はUnite部分で左右をランダマイズするという最悪をして逃げました）

2. CodeForcesでArray.Reverseが使えない

using System;

class TEST{
    static void Main(){
        Sol mySol =new Sol();
        mySol.Solve();
    }
}

class Sol{
    public void Solve(){
        int[] A = new int[]{3,1,4,1,5,9,2,6,5,3,9,8,9,7,9};
        Console.WriteLine(String.Join(" ", A));
        
        Array.Sort(A);
        Console.WriteLine(String.Join(" ", A));
        
        Array.Reverse(A);  // ここでRunTimeErrorになる
        Console.WriteLine(String.Join(" ", A));
    }
}

Monoのバージョンの問題なのか，メソッドが見つからないというRunTimeErrorが投げられます． それコンパイル時に見つけてくれよ．．．Testcase2とかで見つけないでくれよ．．．頼むよ．．．

3. CodeForcesで特定の型のHashSetが使えない

using System;
using System.Collections;
using System.Collections.Generic;
using System.Numerics;

class TEST{
    static void Main(){
        Sol mySol =new Sol();
        mySol.Solve();
    }
}

class Sol{
    public void Solve(){
        
        //TestHashSet((bool) true);
        //TestHashSet((byte) 1);
        //TestHashSet((sbyte) 1);
        TestHashSet((char) 1);
        //TestHashSet((decimal) 1);
        //TestHashSet((double) 1);
        //TestHashSet((float) 1);
        TestHashSet((int) 1);
        TestHashSet((uint) 1);
        //TestHashSet((long) 1);
        TestHashSet((ulong) 1);
        //TestHashSet((short) 1);
        //TestHashSet((ushort) 1);
        //TestHashSet((System.Numerics.BigInteger) 1);
        
    }
    
    void TestHashSet<T> (T addedValue){
        HashSet<T> h = new HashSet<T>();
        try{
            h.Add(addedValue);   // ここでRuntimeErrorになる．
        } catch (Exception e){
            Console.WriteLine(e);
            Console.WriteLine("{0} NG", addedValue.GetType().Name);
            return;
        }
        Console.WriteLine("{0} OK", addedValue.GetType().Name);
    }
    
}

これもMonoのバージョンのせいかわからないですが，ある型のHashSetを作って，そこにその型の値（addedValue）をエントリーすると，型によって動いたり動かなかったりするバグです．

コメントアウトしてあるものが，正常に動かなかった型です．ほとんど動きませんね．．．（2018/12/31 カスタムテストで確認しました） 最悪なのが，インスタンスは確保できるのにAddしようとするとエラーになるところと，エラーがなんなのか例外に投げられないところです．．

（例外キャッチしようとしても中身がなく，Runtime error: exit code is 13131313としか出ない）． long (64bit整数)でも起きるのがとてもつらい．

ちなみにO(1) ハッシュをもつ辞書Dictionary<T,U> ではこの問題は起きないので，本番はそれに逃げました．

using System;
using System.Collections;
using System.Collections.Generic;
using System.Numerics;

class TEST{
    static void Main(){
        Sol mySol =new Sol();
        mySol.Solve();
    }
}

class Sol{
    public void Solve(){
        
        TestDictionary((bool) true);
        TestDictionary((byte) 1);
        TestDictionary((sbyte) 1);
        TestDictionary((char) 1);
        TestDictionary((decimal) 1);
        TestDictionary((double) 1);
        TestDictionary((float) 1);
        TestDictionary((int) 1);
        TestDictionary((uint) 1);
        TestDictionary((long) 1);
        TestDictionary((ulong) 1);
        TestDictionary((short) 1);
        TestDictionary((ushort) 1);
        TestDictionary((System.Numerics.BigInteger) 1);
        
    }
    
    void TestDictionary<T> (T addedValue){
        Dictionary<T, T> d = new Dictionary<T, T>();
        try{
            d.Add(addedValue, addedValue);
        } catch (Exception e){
            Console.WriteLine(e);
            Console.WriteLine("{0} NG", addedValue.GetType().Name);
            return;
        }
        Console.WriteLine("{0} OK", addedValue.GetType().Name);
    }
    
}

他のジャッジシステムでどうかは分からないですが，少なくともAtCoderとTopCoderではArray.ReverseもHashSetも使えましたね．

4. next permutation

前述のArray.Reverseが使えないバグが発覚して，自分のライブラリにArray.Reverseつかってるやつがあるか調べていたら見つけたバグ（？）．C#にはnext_permutationが無いので，自分で実装したものを長らく（4年以上）使っていましたが・・・

using System;
using System.Collections.Generic;

class TEST{
    static public bool NextPermutaion<T>(T[] A)where T:IComparable<T>{
        for(int i = A.Length - 2; i >= 0; i--){
            if(A[i].CompareTo(A[i+1]) < 0){
                int trgt = Array.FindLastIndex(A, x=>A[i].CompareTo(x) < 0);
                Swap(ref A[i], ref A[trgt]);
                Array.Reverse(A, i+1, A.Length - (i + 1));
                return true;
            }
        }
        Array.Reverse(A);
        return false;
    }
    static void Swap<T>(ref T x, ref T y){
        T t=x;x=y;y=t;
    }
    
    static void Main(){
        int[] A=new int[]{0,1,2};
        
        do {
            Console.WriteLine(String.Join(" ",A));
        } while(NextPermutaion(A));
        
        Console.WriteLine("last state:{0}",String.Join(" ",A));
    }
    
}

・・・NextPermutaion ってスペル間違ってるやんけorz...

（ちなみにNextPermutaionで検索すると結構いろんな人がtypoしてツイートしてましたね．．．）

終わりに

いろいろあるけど来年もgood luck, have funしたいね！

プリム法だと思った？残念，ダイクストラでした！

0. 導入

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　やつを追う前に言っておくッ！
　　　　　　　　 ,. -‐'''''""¨¨¨ヽ
　　　　 　 　 (.＿＿_,,,... -ｧァﾌ|　　　　　　　　 　あ…ありのまま 今　起こった事を話すぜ！
　 　 　 　 　 |i i|　 　 }!　}} /／|
　　　　 　 　 |l､{　 　j}　/,,ｨ//｜　　　　　　　『おれはプリム法を書いていたと
　　　　　　　 i|:!ヾ､_ﾉ／ u {:}//ﾍ　　　　　　　　　　　　　　思ったらいつのまにかダイクストラが書きあがっていた』
　　　　　　　 |ﾘ u' }　 ,ﾉ　_,!V,ﾊ |
　　 　 　 ／´fト､_{ﾙ{,ィ'ｅﾗ　, ﾀ人　　　　　　な…　何を言ってるのか　わからねーと思うが
　　　　 /' 　 ヾ|宀| {´,)⌒`/ |<ヽﾄiゝ　　　　　　 おれも何をされたのかわからなかった…
　　　　,ﾞ　 ／ )ヽ iLﾚ 　u' |　| ヾｌﾄﾊ〉
　　 　 |／_／　 ﾊ !ニ⊇　'／:} 　V:::::ヽ　　　　　　　　頭がどうにかなりそうだった…
　　　 /／ 二二二7'T'' ／u'　__ /:::::::/｀ヽ
　　　/'´r　-―一ｧ‐ﾞＴ´　'"´ ／::::／-‐ 　＼　　　　 催眠術だとか超スピードだとか
　　 / // 　 广¨´ 　/'　　 ／:::::／´￣｀ヽ ⌒ヽ　 そんなチャチなもんじゃあ　断じてねえ
　　ﾉ ' /　 ノ:::::`ー-､___／:::::／/ 　 　 　 ヽ　　}
_／｀　/::::::::::::::::::::::::::￣`ー-{:::...　　　 　　　ｲ もっと恐ろしいものの片鱗を味わったぜ…

この記事は「競プロ!!」 競技プログラミング Advent Calendar 2017の19日目の記事です． さて，競プロのアルゴリズムの中で比較的人気の低い（要出典）古典的アルゴリズムに，プリム法というものがあります．

プリム法

アルゴリズムの概略を説明すると，

1. ある頂点vを一つ選ぶ．v１つからなる集合をSとする．
2. Sから到達可能なS以外の頂点のうち，もっとも近い頂点を選び，これをSに加える．
3. 2を実施できる限り2を繰り返す．実施できなくなった時にSがもとのグラフの最大全域木になる

という，証明はさておき標語的にはすごく分かりやすいアルゴリズムです．

コードで書くと（細部は適当ですスミマセン）

class edge{
    int from;
    int to;
    int cost;
}

// 最小全域木を構成する辺のリストを返すメソッド
List<edge> MinimumSpanningTree() {
    PriorityQueue<edge> Q;    // 優先度つきキュー(edge のコストが小さい順に取り出せる）
    bool[] used;              // Sに含まれたかをbool で持つ
    int[] min;                // min[v] は 各タイミングでのSからvへの最小cost
                              //  全要素をinfで初期化しておく
    Edges[] E;                // E[v] には vを始点とするedge (from := v, to, cost) が入っている
    
    used[v0] = true;
    min[v0] = 0;
    foreach(edge e in Edges[v0]) {
        Q.Enqueue(e);
    }
    
    List<edge> MST;    // Sに追加する際に張った辺を入れるリスト
    int tot =  0;      // 各時点での Sを構成するcostの合計
    
    while(!Q.IsEmpty) {
        edge e    = Q.Dequeue();
        int  from = e.from;
        int  to  = e.to;
        int  cost = e.cost
        if(used[to] == true) continue;    //行き先が既にSに含まれている場合は何もしない
        
        used[to] = true;
        min[to] = tot + cost;
        MST.Add(e);
        
        foreach(edge e in Edges[nxt]) {
            if(!used[e.to]){
                Q.Enqueue(e);
            }
        }
    }
    return MST;
}

ところが，このプリム法のコードがダイクストラ法のコードに似ていることが，しばしば話題になることがあります．

class pair{
    int pos;
    int cost;
}
class edge{
    int to;
    int cost;
}

// 始点 v0 からの 単一始点最小コストの全点リストを返す．
int[] Dijkstra(int v0) {
    PriorityQueue<pair> Q;    // 優先度つきキュー(pair のコストが小さい順に取り出せる）
    bool[] used;              // Sに含まれたかをbool で持つ
    int[] min;                // min[v] は 各タイミングでのSからvへの最小cost
                              //  全要素をinfで初期化しておく
    Edges[] E;                // E[v] には vを始点とするedge (to, cost) が入っている
    
    used[v0] = true;
    min[v0] = 0;
    Q.Enqueue(new pair(v0, 0);
    
    while(!Q.IsEmpty) {
        pair p    = Q.Dequeue();
        int  now  = p.pos;
        int  cost = p.cost
        if(used[now] == true) continue;    //行き先が既に最小確定している場合は何もしない
        
        used[now] = true;
        min[now] = cost;
        
        foreach(edge e in Edges[now]) {
            if(!used[e.to]){
                Q.Enqueue(new pair(e.to, min[now] + e.cost));
            }
        }
    }
    return min;
}

差分は，優先度付きキューに辺を入れて取り出すのか，経路長を入れて取り出すのか． なので，結構違うことをやっているのですが，確かに紛らわしいです．

紛らわしさと，それに比べて分かりやすく実装量ももう少し少ないクラスカル法の方が人々には好まれているような気がしますが，今回は記事ネタとして，そこで敢えてプリム法に迫ってみたいと思います．

1. もし，1ミリも最小全域木を求めるアルゴリズムを知らないときに，以下の問題に出会ったら

• N 個の 頂点からなるグラフ が与えられる．各頂点間にはコストを持つ辺がある．
• このグラフの辺をいくつか選び，N個の頂点が連結になるようにしたい．
• コストの総和を最小にしたいとき，その最小値を求めよ
• 制約　N ≤ 15, 辺のコスト ≤ 100000

さて，まず考察すると

• N頂点なのでN-1回つなぐのが最小コストを実現する必要条件．木になるね．
• あるk頂点の木があったとして，k+1番目の頂点を追加するとしたら，一番短い辺でつなげばよさそう．
• 頂点をつないでいく順番で，出来上がる木は違ってそうだけど，k+1番目をつなぐのに際してはそれは関係ない．
• k頂点の木がどの頂点で構成されているかだけが問題になりそう．
• 制約，Nが小さいな．ビットで管理すればいいか．

というような感じで，下図をみます． 右側のようなコスト付きグラフを与えられたときに，最大全域木を見つけに行くためにこのようなDAGを考えることができます．

さて今回の本題，ここでダイクストラをやってみます． プリム法に則って，最初にひとつ頂点を選ぶところは今回は頂点0を選んだところからスタートします．

各頂点から次の頂点に向かう辺は，DAG上では1本になっていますが，実際には 集合から に向かうDAG上の辺コストは の各頂点から に伸びる元のグラフの辺の最も短い辺コストになっています．では実際にやってみますと，

ダイクストラ法は最小コストとなるノードが確定していくアルゴリズムで，赤で囲まれたノードが各ターンでの確定ノードです． 真に最小値が更新されたときに各ノードのコストが青字になっています． 最小全域木が確かに求まっています．

2. 考察が埋まらなかった．

上のダイクストラによって各ノードが確定していく様子を見ているとあることに気づきます．

• 最小コストは1度しか真に更新されない

一番近いところを選んでいけばいいというプリム法が成り立つことから考えると，これは確かに当たり前なのですが，逆に考えるとこの性質がグラフの構成法から従うことが示せれば，つまりプリム法は冪集合DAG上のダイクストラが凄くうまくいく性質を持っていると言えるので，「いやープリム法書くつもりがダイクストラ書いちゃってたわー冪集合上でドヤァ」と言える気がしたのでした．

結局これは正しいとは思うのですが，explicitな証明がつけられなかったのというのが今回大失敗だったという記事でした．なんという低クオリティ．

3. 蛇足：プリム法で得られる最小全域木のサイズが初期値 に依らない説明

とはいっても，上のダイクストラで最小全域木が求まるということは依然として正しい（ただし計算量がアレ）なので，それを使ってプリム法の初期値が何でもいいということだけ説明しておこうと思います．

さて， から1つ頂点を選ぶのをコスト0の辺であらわしていますが，この冪集合DAG全体でダイクストラをしても，結果は1つに定まります．そして，そのようにして得られた最小全域木を経路復元で一つ決めます．全体でダイクストラした場合は以下のようになります．

さて，これは最初の1頂点 から始めた場合の初期値＝頂点1バージョンとみなすこともできます． そこで，他の頂点に対して，もしこの全体ダイクストラで終点=最小全域木から出発して，ノード \}を経てに戻るような経路復元ができるならば，そのを初期値にして求めた最小全域木のサイズは元の最小全域木のサイズに一致します．

これは実は簡単にできます．最初に から作った最小全域木の根として を選び，あとは葉となっているノードを切り離していくことを考えると，このような辺の選び方に対応するDAGの経路は必ず存在するからです．上の絵では，例えば最後に追加された頂点は2ですが，0を取り除いて11110に移動することもできる，という具合です．根は最後まで取り除かれないので，求める復元経路が得られたことになります．これによって，プリム法が初期値に依らないことが示せたことになります．

4. まとめ

考察は筆者の演習問題とします．

なぜｄｐ「やるだけ」なのか ～動的計画法について考える その１～

これは、Competitive Programming Advent Calendar 2016の17日目の記事です。

競技プログラミング（以下，競プロ）においてよく出題される動的計画法（Dynamic programming，通称dp）について，「dpやるだけ」という表現を稀に見かけます．競プロを始めた人のうち，多くの人が（少なくとも自分にとっては）最初の壁のうちの一つと言ってもいいdpというジャンルがなぜ「やるだけ」などというパワーワードを伴ってしまうのか．今回はそういうところから，ふわっと動的計画法について考えてみようと思います．どちらかといえばテクニック的な内容というよりは自分がdpの問題に触れるときに意識しているようなことを書いているだけなので，参考になったりならなかったりすると思いますがご容赦のほど．

動的計画法とは

動的計画法

wikipedia によると「対象となる問題を複数の部分問題に分割し、部分問題の計算結果を記録しながら解いていく手法を総称してこう呼ぶ。」ということです．文面だけ見ると難しそうです．とてもやるだけという感じはしません．

そう思いながらもう少しwikipediaの記事を読み進めていくと，例題としてフィボナッチ数列が出てきます．

// A_0 = 1, A_1 = 1 のフィボナッチ数列 A_n の n番目の値を返す関数
int Fib (int n){
    if ( n == 0 ) return 1;
    if ( n == 1 ) return 1;
    return Fib (n - 1) + Fib (n - 2);
}
/* オーバーフローするから 実用コードでゎない */

多分，動的計画法を調べてここにたどり着いた人のうち少なからずの人が「いや，こんな書き方するかなぁ」って思うのではないかと思います．確かに関数がメモ化してあれば無駄な呼び出しはなくなるかもしれないけど，別にだからと言ってあまりうれしさも無いような印象を受けるのではないでしょうか？そもそも関数で書くかなぁ（完全に私見）

実際，自分がネット漁りしながら勉強していた時はそんな風に思った記憶があって，普通に行列累乗する方法でええやんと思ってました．あるいはwikipediaにも記載のあるような，

// A_0 = 1, A_1 = 1 のフィボナッチ数列 A_n の結果を result[n] に格納する　
int result[1000];
result[0] = 1;
result[1] = 1;
for(int i = 2; i < 1000; i++){
    result[i] = result[i - 1] + result[i - 2];
}
/* オーバーフローするから 実用コードでゎない */

という素直なコードを書いて「わざわざ再帰とか使わないよなぁ」とか思っていたと思います．

さて，メモ化するとか配列で書くということが上の動的計画法のページではクローズアップされていますが，今回の趣旨の上ではそれはそれほど大切ではありません．ただ，このフィボナッチ数列の例にも「dpやるだけ」なのかの兆候はみてとれます．
冒頭から極論ですが，「dpやるだけ」の裏付けは以下の２つのどちらかではないかと思います．

• case 1：（相対的に）実装する段階で解の正当性の考察が完了している．
• case 2：マイクパフォーマンス

元も子もない2つを上げてしまいました．
case 2 については「ハラスメント，ダメ，絶対」の精神でもう各自の裁量に任せるしかないのですが，case 1については少し考察の余地があります．上のコードの例はある意味ではcase 1 で，定義に従って計算しているだけなのですが，それは取りも直さず正当性の考察が完了していると言えます．だって定義に従って計算しているだけだもの（2回言う）．

こういう部分をもうちょっと考えることで，動的計画法の習得の一助になるようなことを考えていきたいというのが本稿の趣旨です．与太話感がパないですが，それぞれのレベルで感じることを書くのもアドベントカレンダー記事っぽくてよいかと開き直ります．なにより「dpやるだけ」と（口に出さないまでも）感じられるようになるというのは，そこまで悪いことだとは思わないので，その瞬間を得るための考え方の指標とかを示すのを目標に．

今そこにある動的計画法 ~Clear and present dp~

こんな問題を考えてみましょう．

• サイズ N の intの配列 A[N] が与えられる．
• 与えられた配列の中身のうち，最大値を求めよ．

　制約　1 ≤ A[i] ≤ 100000, 1 ≤ A[i] ≤ 100000000 ( 0 ≤ i < N )

素直にコードを書くとこんな感じのコードになるのではないでしょうか．

// 要素数 N の配列 A の最大値を求めて返す
int MaximumOfArray (int A[], int N) {
    int max = -99999999; // Aのどの数字より必ず小さい数値で初期化
    for(int i = 0; i < N; i++){
        if(A[i] > max) {
            max = A[i];
        }
    }
    return max;
}

ね，簡単でしょう？これならやるだけと言ってしまう気持ちもわかる（？）
冒頭で「動的計画法は難しそう」と書きましたが，これは立派な動的計画法です．
どう考えるのがいいのかというのがありますが，wikipediaの定義を満たすかという観点で言えば

• point 1 :「対象となる問題を複数の部分問題に分割」
• point 2 :「部分問題の計算結果を記録しながら解いていく」

この2点を確かに満たしています．

• point 1 について：ループを順次回している部分に着目すると，「\( 0 \)から\( N - 1 \)までみる」という問題を「\( 0 \) から \( i \) （ \( i ≤ N-1 \) ）までみる」という問題に分解している．
• point 2 について：\(0\)から\(i-1\)までみた計算結果が 変数 max に入っているのを，\(i\)番目のループで利用している．

ここで最も「動的計画法」だなぁと思う点は，max という変数が移り変わっていくところです．移り変わっていくといっても，ランダムに変わっていくわけではありません．そこには純然たるルールがあります．例えばループが\(i\)で止まった時にmaxに入っている値は何かと聞かれれば，それは明確に決まっています（今回の場合，「\( 0 \) から \( i -1\)までみた最大値」です）．逆に言えば，あるルールで情報を伝えていった先に答えが見つかる，そのようなルールを決めている，といえます．

情報を余さず届かせる

同じような例ですが，見方を変えて以下のような問いを考えてみます．

　あなたはすっごいものぐさな40人の生徒からなる学級の担任の先生です．さて，今日あなたは先日採点したばかりのテストを皆に返却しました．
　ところが，うっかりもののあなたは，クラスの最高点を調べておくのを忘れてしまいました．
　そこで，生徒たちから得点を聞きたいのですが，生徒は皆，「点数は覚えてるけど，テスト用紙はもうカバンにしまってしまって出すのがめんどくさい，てゆーか先生のところまで行くのもめんどくさい」と非協力的です．
　一方，あなたも負けず劣らずものぐさのため，一人ひとりの机に赴いて点数を訊くなどということはする気がありません．
　そこで，教壇からふんぞり返って「わかった，じゃあ今から私が指名するから，指名された人は前後左右隣の人に点数を訊いて，それと自分の点数を比べて一番高い点数だけ覚えておいてくれたらいいわ」と宣言しました．
【問題】どのように指名していけば，最終的にクラスの最高点が教壇から動かなくてもわかるか，その順番を答えてください．

最終的に図中の21番太郎君に訊いて答えを知りたいとして，どういう順番に聞いていけばいいかという問題．
まぁ答えはいくつもあります．例えばこんな感じでしょうか？

見た目はまぁまぁ一見全然違いますが，どちらの回答でも最終的に21番太郎君に訊くとクラスの最高点を知ることができるでしょう．

さて，ここで少し自問してみて欲しいのですが，指名された生徒の一人一人は前後左右の生徒と自分の点数を比べて（時には自分の点数すら忘れて）その中で一番大きい数字を覚えるようにしているだけです．それを何らかのルールに則って順番に実行させることで，あなたはクラス全体の最高点を知ることができています．さらに言えば，解答例１の薄緑の線を省略しても大丈夫そうと考えることもできるかもしれません．しかし大切なことは，生徒たちに許された動作を考慮したときにどう順番に実行すれば，余さず必要な情報を手元に届けられるか，ということです．今回の問題の場合，クラスの誰が最高得点を得ているか分からないので，全員を経由していることと，それが最終的に21番太郎君の所まで運ばれてくること，です．極端なやり方を挙げれば，1から40までの順に機械的に指名するというのを40回繰り返してから21番太郎君に訊くのでもいい．

" 何"を，" どう" 伝えるか!? ~「状態」と「遷移」 ~

本記事のテーマが「なぜdpは「やるだけ」なのか」という事だったので，いかにも簡単すぎる題材を選んでみたのですが，競プロにおける多くのdpの問題はこのような" 何"を，" どう" 伝えるかという部分を考察することを必要とします．この”何”にあたる部分を「状態」，"どう"にあたる部分を「遷移」と呼びます．（上の例だと，40人の脳内に何の数字があるかという情報が「状態」，{前後左右に訊いて最大値を覚える}と{それを実施する順番}が「遷移」にあたります）

dpの問題はこの「状態」と「遷移」をペアで適切に決める問題と言えます．もちろん，問題によって状態や遷移が自明に決まっているものもあります．例えば最初のフィボナッチ数列の例は，値が状態にあたり，漸化式が遷移にあたる上，疑問の余地なく定義されているので，自明と言ってもいいかもしれません．ただ，多くのdpの問題は両方を決めることを要求されます．またこの２つは独立にそれぞれ決められるわけではなく，最終的に得たい情報を得るためにペアで上手くいくように適切に決めてやらなければなりません．

おそらく一般的には「状態」を適切に設定することが難しいです．「遷移」は自分の行動にあたるので，（効率的かはともかく）何かを挙げることは可能なのだけれど，遷移ドリブンで考えると適切に状態を定義できなかったり広くなりすぎたりしてしまいます．かといって必要な情報は網羅していないといけない．逆に言えば，適切に状態を設定できるということに正しく遷移させられるという要求が含まれます． 上の40人学級の例で，どう遷移を選ぶかという問題に対して割といろいろ考えたり工夫することができるのも，すでに状態が設定できているからとも言える．

ようやく冒頭のcase.1について述べることができます．

• （相対的に）実装する段階で解の正当性の考察が完了している．

どんな問題も，解の正当性の考察が完了していれば，そりゃあとはやるだけでしょと言えるでしょう．それがなぜdpで（相対的に）顕著なのかという点を考えると，dpで解ける問題は，上のように「状態」と「遷移」の2つを決める必要がある．2つも決めないといけないのだからほかの問題に比べると分からなければ手の付けようがないのだけれど，逆にその2つ，とりわけ「状態」を適切に決められた時には遷移も混みで考察出来ているため，いうなれば解のダブルチェックが出来ている状態です．なので安心感があり，実際dpの問題は提出できればACできることが多い気もします．
(個人的には，正しく推移できているかというチェックは数学的帰納法のプロセスそのものなので，解きながら証明も進んでいくお得感があると感じることさえあります．逆にdpがある程度解けるようになると今度は貪欲法が難しいと感じるようになるケースは，遷移ドリブンで考えてしまっているケースが多いのではと思ってます)

そして更に，上に書いたようにdpの難しさは「状態」の設定にあるので，いいかえれば場面場面に応じたテクニカルな「状態」の設定方法が先人の知恵，典型的なアルゴリズムとしていろいろ名前がついています．テクニカルなので，最初は思いつかなくて当然です．しかしテクニックなので，一度習得してしまえば応用が利き，かつ遷移後の状態が求めるものかどうかがすぐに分かるようになります．（ちなみに私が最初に感銘を受けた状態設定をもつdpはナップサック問題でした．そのあたり次章で書きたいと思います）．なので，見知ったdpの問題に帰着できた場合にも，実績あるアルゴリズムだからというよりは，「どう推移するかが頭の中で完全に把握できる→正当性が保証される」が引き金となって，ああやるだけだなぁと思ってしまうのではないでしょうか．

ということで，この記事の結論としては敢えて，
　dpは「状態」と「遷移」を正しく決められれば，正当性が保証されるので，やるだけ
としたいと思います．出来るとは言ってないしこれトートロジーですよね

なので，dpがイマイチ得意でない人や例題は分かるんだけどという人は，状態と遷移を意識して考察してみると幸せになれるかもです．（私がそうだったという話）
そうはいっても漠然としているので，状態と遷移について続いて記事を書く予定です．

アドベントカレンダーも終盤戦に差し掛かってきました．明日はroiti46さん（CPACその１）とcamypaperさん（CPACその２）です．楽しみですね！

ダイクストラ法が分からなかった君のために

これはCompetitive Programming Advent Calendar 2015 の19日目の記事です。

さて、表題の通りこの記事はダイクストラ法についての思い出を語るものです。
競プロライフも2周年を迎え、取り組み始めたころに比べればかなりいろいろな問題も解けるようになりますます楽しくなってきたのですが、最初の頃割と長い間しっくりこないというか苦手意識のあったダイクストラ法について、振り返りながらいろいろ書いてみようと思います。
対象としてはダイクストラが分からなくてググるくらいの人も想定しています。ので多少くどい感じですがご容赦のほど。あともし大きな間違い等あればお知らせください。

ダイクストラ法とは

ダイクストラ法 - Wikipedia

いきなりwikipediaを貼ってしまいましたが、グラフにおいてある頂点から別の頂点への最短距離を求める問題（単一始点最短経路問題）についてのアルゴリズムのうちの一つです。例えば下の絵のような状況を考えます。

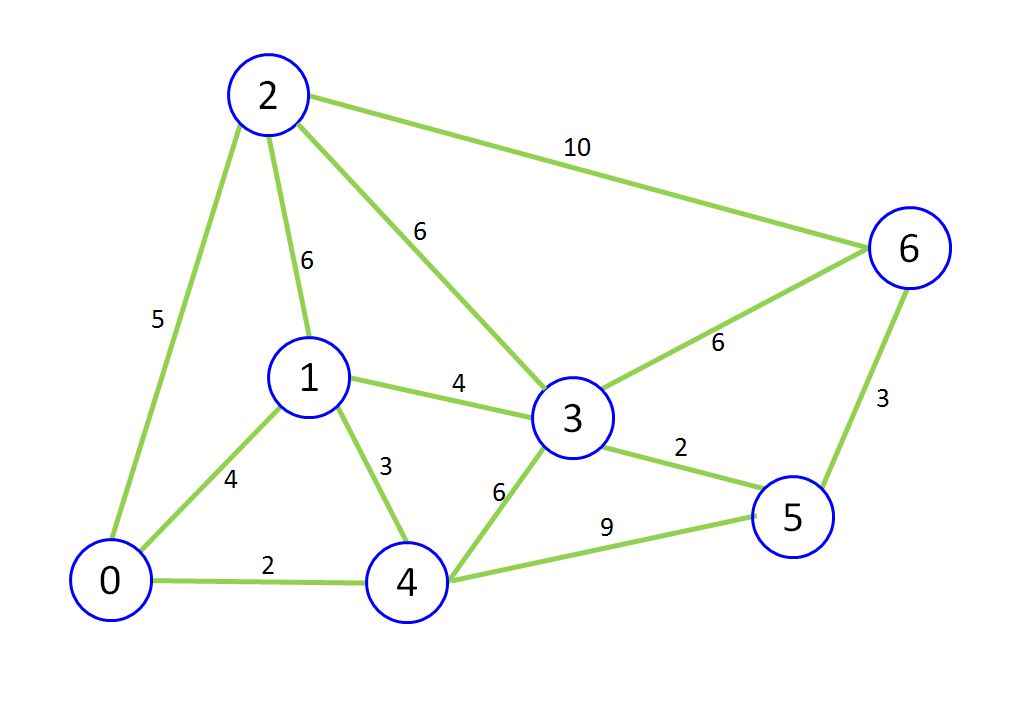
青丸を「頂点」、緑線を「辺」と呼びます。絵から想像できるように、ある頂点から別の頂点には辺を通ってのみ移動できるという状況です（あるいは、移動できる頂点間に辺が張られている）。各辺に付随している数を「コスト」とよび、この辺を移動するのに必要なコストを表しています。単一始点最短経路問題は、ある頂点から別の頂点への移動手段のうち、もっともコストの低い経路（のコスト）を探す問題です。

例えば、頂点を都市、辺を交易路、コストを交易路の距離とすれば、都市0から都市6へ行くにはどの交易路を選んでいけば最短距離でたどり着くことが出来るか、という問題になります。あるいは、頂点を駅、辺を路線、コストを運賃だと思えば、駅0から駅3へは最低いくら必要か、という問題にもなります。古典的問題のため、そのままコンテストで出題されることもさることながら、何を頂点、辺、コストと見立てるかによって応用範囲が広く、いろいろなケースで出題されることのある題材です。以下では頂点の個数を\( V \)、辺の本数を\( E \)で表します。

そもそも、どうやって求めるべきなのか

とりあえず最初に考えるのは、とにかく全ての経路をたどってみて一番短いものを選ぶという事です。

 頂点0から頂点6に向かう経路は、同じ頂点を2回通らないという決まりだけで列挙すると40通りあるようです。これがでも次のようなグラフだとどうでしょうか。

コストを省略していますが、どの頂点からどの頂点にも辺が張ってある場合です。この時、頂点0から頂点6に向かう経路は（同じ頂点を2回踏まない制約があっても）326通りあります。一般に頂点が\(V \)個あるとすると、このように全ての頂点間に辺が張ってある場合は同じ頂点を2回踏まない制約でも \( \sum k ! (k=1,2,\dots,V-2) \) 通りの経路が存在します。これは莫大な量で例えば\( V=100 \)程度でも\( 10^{153} \)程度の数になります。ピンとこないくらい大きな数字です。よく言われる目安として現在のCPUは1秒間に大体1億回（ \( 10^8 \)回)の計算ができると言うところから考えるとヤバさが分かると思います。1年かけても高々31536000秒です。

計算量のオーダーでいうと、\( O(V!) \) 程度になります。階乗はマズイやつですよ。。

最初の例に戻ると、仮に最短経路長が13だと分かっていれば、例えば経路探索の途中で15や16に既に達している場合はその先に進む理由がないので、その部分は枝刈りすることが出来ます。しかし、最短経路やそれに近い少しだけ遠回りが複数あるような場合は、ギリギリまで最短経路長を更新するかどうかわからず、結局上のように膨大なルートを検索しなければいけません。困った。

動的計画法のこころ　～これ、単一始点最短経路"長"問題じゃね？～

最初の例をもう少しよく眺めてみます。最短経路はどうやら2つあり、

• 0 ⇒ 1 ⇒ 3 ⇒ 5 ⇒ 6
    +4    +4    +2   +3
• 0 ⇒ 4 ⇒ 3 ⇒ 5 ⇒ 6
    +2    +6    +2   +3

となっているようです。さて、頂点3まで到達してしまうとあとは頂点5、頂点6とたどるしかないのですが、頂点0から頂点3にコスト8 で到達する道のりが2つあるために、頂点0から頂点6への最短経路自体の個数も増えているようです。

ここで動的計画法のこころが降りてきます。頂点3に辿り着くとそこから頂点5⇒頂点6と進むのが最短であるならば、頂点0から頂点3に辿り着くすべてのコスト8の経路はもれなく頂点0から頂点6への最短経路の一部になります。このことを考えると、経路そのものが大切なのではなく、どの頂点にいくらのコストでたどり着けるのかが大切であることに(天啓によって）気づきます。あるいは、ある頂点に対してあるコストで到達できる経路全体を同一視して、（頂点，コスト) という組に代表させると言い換えてもいいかもしれません。

そうだとすると、各頂点に対して次のような星取表を作って埋めることを考えてみます。（これはいわゆる配るDPと呼ばれるものです）

 

横軸に頂点番号、縦軸にコストを取り、もしそのコストでその頂点に到達できることが出来るならそのマスを塗っていきます。スタート地点には必ず立てるので、コスト0で到達していると考えます。さて、頂点0からは

• コスト4で頂点1へ移動できる
• コスト5で頂点2へ移動できる
• コスト2で頂点4へ移動できる

ので、それぞれ移動できるところに色を塗りましょう。

このような操作

• 「ある頂点にコスト \( k \) で到達できるならば、その頂点から辺が出ている頂点に、コスト ( \( k + \) その辺のコスト) で到達することが出来る（ので色を塗る）」

を"配る"と呼ぶことにします。今回の例では、辺のコストは全て0より大きいので、配り続けていくと塗られるマスはどんどん上に向かって伸びていきます。なので、下からローラー作戦で配って行けば、塗りもらしなく星取表を埋めていくことが出来そうです。やってみましょう。

こうやって表にしてみると、例えば頂点1に辿り着くことのできるコスト（の集合）は\( \{4,5,8,9, \dots \} \)という事が分かります。頂点1に辿り着く最短コストはこれらの中の最小値なので4、という事になります。同様に、確かに頂点6に辿り着く最小コストは13になっています。

回りくどいように見えますが、実は計算量と言う点ではこの時点でかなり効率化されています。縦方向にどこまで配り続ける必要があるかと言う点は現時点では不明なので、これを\( D \)と置きます。横方向に1回走査すると、各頂点からすべての辺が1回ずつ登場しているので、計算量は\( O(E) \)となり、縦方向は\( D \)回配るとすると計算量は\( O(D \times E) \)になります。

\( D \)の上界ですが、例えば各辺のコストが高々\( K \)くらいだとすると、辺全部を足しても\( K \times E \) なので\( D=K \times E \)くらいに取っておけば絶対大丈夫でしょう。すると\( O(D \times E) ＝ O(K \times E^2) \)くらいです。\( E \)はせいぜい\( V \times V \)なので、大体\( O(K\ \times V^4) \)くらいの計算量になります。\( V=100 \)で経路を数え上げると\( 10^{153} \)くらい必要だった計算量は\( K \times 10^8 \) くらいまで減る見積もりになります。大体\( K \)秒くらいで終わりそう。だいぶ絶望感がなくなってきた？

効率よく次を探す　～ダイクストラ法その１、その２～

上の方法でやっていけば現実的な時間で終わりそうですが、いくつか課題があります。

• 辺のコストが大きいとそれだけ時間がかかる
• 辺のコストが整数でないと使えない

\(D\)が扱う辺のコストに左右されて不当に大きくなることで全体の計算時間が増えるのはいただけない。また、コストが整数でないと使えないというのは、例えば小数なら全体に10の何乗かを掛けて整数にしてしまうと言う手もあるかもしれませんが、\( D \)がやはり大きくなってしまったり、また例えばXY平面上の距離のような無理数だと大変苦しい。

そこでもう一度上の図をグッと睨んでみると、いろいろと非効率な部分が見えてきます。そこをもう少し効率化することを考えましょう。

コストの低い方から順番に配ることによって、各頂点に対してその頂点に到達することのできる経路コストの候補がどんどん列挙されていきますが、列挙されたコストのうち最小のものが決定するタイミングはいつになるか、と言う視点で上の星取表を眺めていると、各頂点に対して最初に配る側の立場に立ったマスが最小コストを表していることが分かります。例えば下の図において、（頂点3，コスト8)というマスは、（頂点4，コスト2)というマスから配られて色を塗られますが、頂点3への最小コストが8だと決定するのはあくまで（頂点3，コスト8)というマスが配る側の立場に立った時です。

　

つまり、下から順に見て行って、「初めて配るマス」を順に決めて行けば効率よく最短コストを確定させながら表を埋めていけそうです。「初めて配る」立場に立つ、というのは言い換えればもうそれより手前のマスから配られることは無い、ということなので、ある頂点から配り終わった後、配られたマスのうち、まだ配ったことのない頂点の中から一番手前にあるものを選べばよいということが分かります。

ダイクストラ法が行っているのはこの操作になります。この方法であれば縦方向の \( D \)が整数でなくても良いし、どんなに大きな数でもそれで計算量が変わることはありません。ただし、次の候補が上にあることが前提で探すため、負コストの辺があるときはうまくいきません。

ダイクストラ法（その１）　横方向に探す

既に配られたマスの中で、まだ配ったことのない頂点の中から一番手前にあるマスを探す、という処理をすなおに考えると、\( V \) 個の頂点を一つ一つ確認してまだ配ったことのない頂点の中から最小の到達コスト候補を持つ頂点を選べばいいです。表でいえば横方向、頂点ベースで探すということになります。これがいわゆるオリジナルのダイクストラ法の方法です。

下の図では、既に配り終えた（最短コストが確定した）マスはFixに○が付いています。Fixしていない頂点から一番小さいコストを探して、ピンクのはこで囲っています。

計算量は、 \( V \)個の頂点をチェックするという処理を \( V \)回行うため、この操作だけで \( O(V^2) \) のオーダーになります。配る操作が各頂点ごとに発生するのですが、各頂点から各辺は1回だけしか配られないことを考えると、配る操作のトータル計算量は \( O(E) \) 、アルゴリズム全体では \(O(E+V^2) \) になりますが、\( E \) は高々 \( V \times (V-1) /2 \) なので \(O(V^2) \) となります。また、実際にプログラムに書く際にはこのような表をつくる必要はなく、最小コスト候補だけを覚えておけば事足ります。

ダイクストラ法（その２）　縦方向に探す

同じように、次に配る頂点を今度は縦方向、コストに着目して探す方法を考えましょう。要はいままでに配られたマスの中で一番手前にあるマスを選べばいいのですが、例えば既に \( V_0 ( \leqq V ) \) の頂点から配られているとすると、最大 \( {V_0}^2  \) 個くらいのマスが候補にあるため、それらから単純に一番手前のマスを選ぶというのは場合によっては \( V \)個の頂点を確認するより時間がかかりそうです。そこで優先度付キューを使います。優先度付キューは、\( N \) 個のキューに掘り込まれたものの中から一番小さいものを \( O(log( N )) \)の計算量で取り出すことが出来るキューです。これを使えば今までに配られたマスのうち、まだ配ったことのない頂点を探すことが効率的に行えます。（取り出したマスがまだ配ったことのない頂点なら採用して配る、すでに配ったことのある頂点なら捨てる）

下の図では、ピンクの箱が優先度付キューから取り出されたマスを、赤の箱が優先度付キューに追加された（エンキュー状態の）マスを表しています。

計算量を考えるにあたって、ここではオーソドックスな優先度付キューを採用することにして、キューの保証する性能として\( N \) 個追加されている状態からの要素の取り出し、要素の追加にそれぞれ \(O(log(N)) \)かかるものとします。

まず配る操作が各頂点ごとに発生するのですが、配る操作は優先度付キューへの追加に相当します。一番最悪な状況を考えると、最後の頂点の候補を取り出す時にそれまでの全ての辺を通じて配られたマスがごみとしてキューに残っている状況が考えられるため、キューへの追加に\( O(log(E)) \)かかると見積もっておけばよさそうです。配られるマスの数は各辺が1回だけなので最大\( E \) と考えると、配る計算量のトータルが\( O(Elog(E)) \)になります。

あとは取り出す動作ですが、これも最低 \( V \)回は取り出さなければならないことを考えると、\( O( V log(E) ) \)は必要ということになります。ただ、確定済みの頂点もキューに放り込まれていることを考えると、pop(取り出し)の回数は厳密には \( V \)より多くなると考えられます。これを\( V^{*} \)と書くことにして、\( E \) で抑えられると思っておきます。

2つの合計として計算量は \( O(E log (E) + V^{*} log(E)) \)となります。\( V^* \leqq E \)と\( log(E) \leqq 2 log (V) \)で抑えたとすると \( O(Elog (V)) \)が保障されると考えていいでしょう。

その２の方法の良く知られた高速化として、最小コストが更新される可能性のある場合だけキューに追加するというものがあります。これはキューにたまるゴミが減ることがもたらす効果になります。

（その２の方法の小手先の高速化として、全頂点確定したらwhileのループから抜けるというのがあります。優先度付キューをpopで空っぽにするのは意外と時間かかるよ！）

あと、さらに縦方向にさがすキューを高速化した特別なケースとして、縦軸が非負整数の場合にyosupoさんのスライドで紹介されているRadix Heapの方法があります。

色々なダイクストラ高速化

(あと余談ですが、C#には優先度付キューが標準ライブラリにないので自作せねばならず、いまから未知のアルゴリズムを勉強するのにライブラリも作らなあかん、というのがいくらか障壁になっていたことも書いておきます。そういうやつは逆に道具をそろえるとやる気になるので、ピンチはチャンスの精神で）

効率よく表を埋める　～ベルマンフォード法・SPFA～

最初の表に戻ってもう一度考えてみると、他の単一始点最短距離"長"問題のアルゴリズムについても同じようにこの表を効率的に埋めているのだと考えることが出来ます。

ベルマンフォード法　～そんなD回もまわさんでええんやで～

配るDPでとりあえず距離\( D \)を上限にして1から回していきましたが、実は頂点数 \( V \)に対して、 \( V-1 \)回回せば十分と言うことが、やはり表の動きをグッと睨んでいると分かります。

現在自分がある頂点にいたとして、1回表を横に走査するという操作は、その頂点から1歩動くことを意味します（当たり前）。なので、最短経路を探すに当たり同じ頂点を2度訪れることはありえないことを考えると、最大\( V-1 \) 歩しか進まないはずで、逆に最短経路が\( N ( \leqq (V-1) ) \)歩で達成できるとすると、上のDPローラーが始点含めそれより前の \( N \)点の頂点と到達コストのそれぞれを踏みさえすればいいことが分かります。

「そんな都合よくローラー走査すべき行がみつかるかいな」と思うかもしれませんが、実はこの表の特定の行を走査する必要はありません。配る頂点で本当に必要なのは、最小コストの頂点だけです。なので、毎回のローラー走査では最小候補となるマスからだけ配っておけばよいです。

下の図では、最小コストの頂点から配っていく様を表しています。緑色の線が、最小値を更新するポイントを表します。

（頂点のナンバリングが悪くて、ローラーの横方向を昇順に走査すると1順で全ての最短路が列挙されてしまいました。下は同じグラフで降順に走査した場合です）

計算量は、最大 \( V-1 \)回の操作を必要する場合があることから \( O( (V-1) E) = O(VE) \)になります。ただ、上の図を見て分かるように、ローラー走査する回数は最短経路を実現する歩数の最大値なので、場合によっては途中から同じ動きの繰り返しになります。なので実装ではローラー走査一回ごとに前回との差分が生まれているかをチェックして、更新が無ければその時点で打ち切るのが一般的です。ダイクストラには劣りますが、辺の値とコストしか見ていないため負辺があっても"正しく"動作するため、負閉路検出等への応用があります（すみませんここ勉強不足なのでまたどこかで・・・）

SPFA　～もうちょっと効率化してみる～

基本的にベルマンフォード法の方式で上の表を埋めるにあたって、別にすべての辺を走査する必要はないよねというのがSPFAの動作になります。一回配る立場に立った頂点からは、その最短コストが次に更新されるまでは配る必要がないはずです。

配られていない頂点はまだ配ることができないので、配られた頂点だけが対象になるのでこれをキューに入れて管理します。また、各頂点の最小コストだけ分かっていればいいので、それは別で管理しておきます。ダイクストラの場合は、「頂点とコストの組」を優先度付キューに入れておかなければ意図した頂点が見つからないため、キューの外で管理することはできませんが、SPFAの場合はとにかく配れれば良いのでキューには頂点だけを入れればよいです。言い換えれば、「頂点とコストの組」をキューしたつもりになっておいて、その頂点がキューから取り出される前に最小コストが更新された時は、キューされた「頂点とコストの組」のコストが書き換わったと考えればいいということでもあります。そのため、エンキュー状態にあるかというフラグも各頂点で持っておきます。

このようにしておけば、ベルマンフォード法においてもう配る必要がなくなった頂点が除外される分だけ効率的になることが分かります。ただ、例えば\( n \)歩で見つかった最短経路長候補が \( m ( > n ) \)で更新された時に、既にキューからその頂点が取り出されていた場合は再度エンキューされるため、ダイクストラ法のように最初にキューから出てきたときに最小コストが保障されるわけではないことに注意が必要です。

分かりにくいですが、赤い箱がエンキューを表しています。エンキューされた状態で最小コストが更新された場合も同じように赤い箱で囲んでいますが、キューの中身は変わっていません。また、頂点6に着目すると、コスト14のところからと、コスト13のところと2回配っているのが分かると思います。

 計算量ですが、ベルマンフォード方式よりは速そうだけど、言っても枝刈りなのと、いかにも\( O(VE) \)のオーダーでないと計算できない例が作れそうなので、最悪\( O(VE) \)という気がします。ここによるとランダムケースでは\(O(E)\)のオーダーらしいです。うーんこれはちゃんと証明見ないと分からないなすみません。

あの、結局僕はどういう経路を通ればいいのでしょうか（哲学）　～経路復元～

単一始点最短経路"長"問題じゃね？と思い直してから、効率的に最小コストを求めることが出来るようになりましたが、じゃあ実際どういうルートをたどればそれが実現できるのよ？という問いがまだ残っていました。しかし最初に述べたように最短経路自体は、なんの制約もなければ山のようにある可能性があります。どうしたものか。

実は、どのアルゴリズムを使っても、全頂点に対して始点からの最小コストが求まっていることに気づきます。これをうまく利用することで、一歩一歩が確実に最短経路から外れずに目的地に向かっているかを判定することができます。ポイントはゴールから逆算するというところ。ゴールを始点にして、各頂点への最小コストを求めておきます。以下のように判定しながらゴールを目指せばいいです。

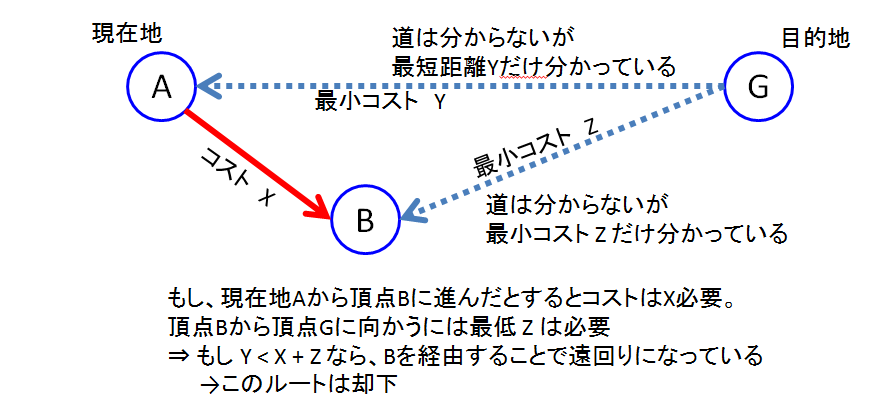
最悪計算量として\(O(E) \) くらいで見つかります。人生もゴールからの逆算で今のふるまいを決めていければいいのにねとおもわないでもないが、最小コストで行けばいいというものでもない。

で、どれがいいのよ？　～ベンチマークしてみる～

さて、これら4つのパフォーマンスについて、せっかくなのでベンチマークしてみました。

表中の系列はそれぞれ

• Dijk1 \( O(V^2) \) ダイクストラ，
• Dijk2 \( O((E+V)logE) \) ダイクストラ
• Dijk2 \( O((E+V)logE) \) ダイクストラ・枝刈りあり
• Berm \( O(VE) \) ベルマンフォード
• SPFA \( O(VE) \) SPFA

で、各グラフの

上段は横軸が頂点数　\( V, ( 10 \leqq V < 4000 ) \)　、

下段は横軸が辺の数　\( E, ( V \leqq E < V*(V-1)/2 ) \)　

で縦軸がそれぞれ計算に要した時間[msec]になります。

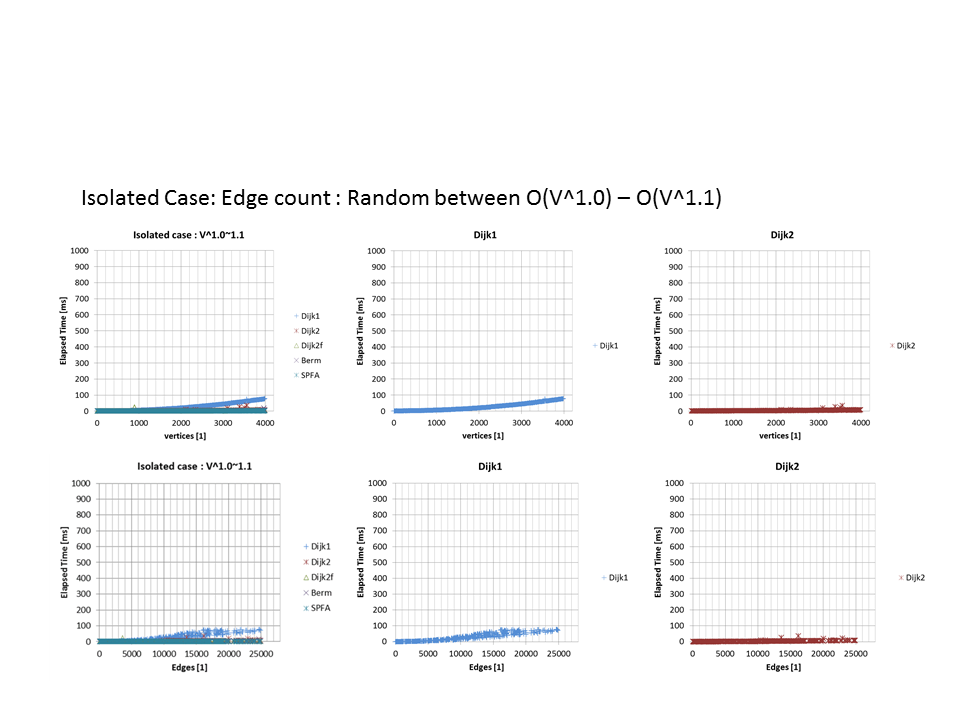
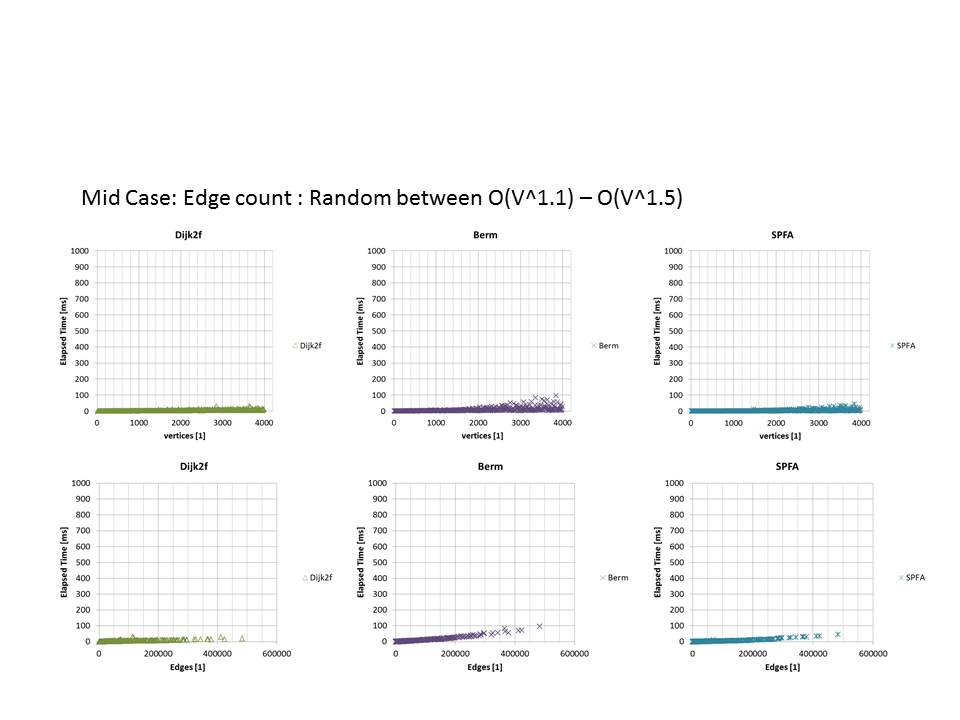
うーん、これだけ見ると枝刈りダイクストラ一択って感じだけど、ベルマンフォードとSPFAが思ったより速いのが結構意外という気がします。適当なランダムケースだからかなぁ・・・あと確かに \( O(E) \)っぽくなってる。

枝刈りしない優先度付キューはヤバい。枝刈りしよう。

以下、辺の密度ごとのプロットも載せておきます。確かに疎なケースでは \( V \) 成分が　\( O(V^2) \)　ダイクストラだけ見えていたりしてなかなか面白い。

一応ソースコードのリンクを載せておきます。適当なC#なので読めればいい人向け。。

CPAC 2015のベンチマーク用ソースコード · GitHub

参考にしたページや問題など

参考：

色々なダイクストラ高速化

SPFAの紹介 - hogloidのブログ

2011/12/19 - Leftist Heap & Skew Heap

ダイクストラやってみたい方向け

Programming Problems and Competitions :: HackerRank　延々ダイクストラやる

No.160 最短経路のうち辞書順最小 - yukicoder　経路復元

Winter Bells | Aizu Online Judge　経路復元＋数え上げ

おわりに

単一始点最短距離問題の代表的アルゴリズムであるダイクストラ法について、理解に至るまでいろいろ考えたことを振り返りながらまとめてみました。

競技プログラミングをやっていく中で多分多くの方が動的計画法につまづくと思い、最初は同じ題材で「古典的アルゴリズムに学ぶ動的計画法のこころ」という記事を書こうとしていたのですが、いつの間にかタイトルが変わり中身も変わってしまいました。とはいえ、かなりの紙面を配るDPに割いたので、なにかつまづいている人の理解の一助にでもなれば望外の喜びです。たとえばDPの表の縦軸をbitで管理した訪問済み／未訪問の値にして色を塗っていけば巡回セールスマン問題になったり、色を塗るというboolの部分を最小コストに置き換えて行ったり。いろいろとバリエーションはあるものの、「上手く問題を置き換えてまずローラー作戦する土壌を考える→重複や要らない情報を削ったり、データ構造をうまく使って計算を高速化する」という流れは、DP問題を解く王道パターンなので。

と、思っていたのに途中からアルゴリズム比較の方が面白くなってきてこんな記事になったという次第です。

ではでは。

明日（まぁ、記事公開は間に合っていないのですが・・・）の担当はHiroyuki Sanoさん（CPACその１）とMさん（CPACその２）です。お楽しみに！

社会人10年目から始める競技プログラミングのすすめ

これは、Competitive Programming Advent Calendar 2014の17日目の記事です。

競技プログラミングという世界を知って1年がたちました。結構飽きやすい性格の自分が1年ほどコンスタントに参加するという充実したプロコン（プログラミングコンテスト）ライフを送ることができた記念に、これからプロコンに参加してみようという方向けの記事を書かせていただきます。CPAC2014参加諸氏のような技術的に高度な内容は残念ながらなさそうですが（書けるものなら書きたい）、10年目エンジニア的視点で自分が感じたことを踏まえて「これはいいものだ」と思えたところなどを中心に振り返ることで、なんとかタイトル詐欺を回避したいと思います。中盤はお目汚し感が強いかも。。

経緯や参加したプロコンなど

半導体関連のメーカーで開発の仕事に従事していますが、2012年に職場都合で富山県に引っ越すことになりました。初の関西脱出というところで最初はわくわくしたものの、その後、富山人ライフにも飽きが来ていた2013年の春ごろにFacebookの友人の記事でcodeiqを知ったのが原初体験だったかと思います。

codeiqの出題者や参加者の中にはもちろん競技プログラミング経験者も多いようで、その情報をたどるうちに知ったのがAOJです。しばらくはAOJをコツコツと進めていましたが、割とすぐに解けない壁にぶつかります。回答公開されている方のソースを読んでもよく分からない。そう、動的計画法です。どうやら未知の考え方があるみたい。

分からないのでググったりしているうちに出会ったのがAtCoderですね。というか多分最強最速アルゴリズマー養成講座などの記事から知ったのだろうと思います。この記事か何かでTopCoderの存在を知って、あとCODEVSという学生プログラマのAIコンテストの配信を見たりして、コンテストも挑戦してみようと思ったあたりからいわゆる競技プログラミングの世界に足を踏み入れはじめます。ただ、TopCoderは言語がC++/Java/C#と限定されていた一方、僕はC言語でホントにちょっと書ける程度だったので、しばらくAOJでC#に慣れるために練習しました。

 SRM（TopCoderのアルゴリズム競技部門）初参加は2014年の1月の下旬、easyを128/250pts位で通して、灰色コーダーデビュー。Ratingの重みを知ります。Ratingは命より重い。嘘です。嘘ですが、プロコンの中毒性をエンハンスしている大きな要素の一つであることは間違いないです。それと、中毒性という点では決まった時間で問題を解くというところが学生時代の試験を思い出して、これもまた懐かしい感覚です。

SRMは代表的なプロコンですが頻度は隔週弱くらいなので、経験を積むという意味でもっとオンラインコンテストないか、と探してみるといろいろあります。codeforcesが高頻度でコンテストを開催していて、こちらは隔週よりかなり多い印象です。codeforcesに関しては、初参戦から4回くらい参加した後、運営側のトラブルで2週間くらいのデータが復元不可能になるほど壮大にこどふぉる（後述）事件がありアカウントごと消えたりしました。初回の結果でスタートのRatingが決まるので、2回目の登録の時、「再履修アドバンテージでハイスコアスタートでいきなりdiv1ワンチャンあるんじゃね？」と思ったがまぁそんなことはなかったです。

そんな感じでSRMとcodeforcesをメインに取り組んでそろそろ1年です。他に手を出してみたところではHackerRankやProjectEulerなど、まだまだたくさんあります。最近ではyukicoderさんにかなりお世話になっています。

面白いの？

個人の感想であり、効果には個人差があります。エッセンスを説明するのにちょっとしたゲームをしてみます。 

16個の数値と、それぞれに振られた番号が上の図のように与えられています。また、あなたの手元には電卓とメモ帳があります。
これから100問あなたに質問します。1問の質問は簡単で以下の要領です。

• 2つの番号 A,B (但しA ≦ B)をこちらが指定します。番号Aから番号Bまでに対応する数値の総和を答えなさい
• (例) 問0：1～4　⇒ 8+14+9+19 = 50 

さて、電卓をたたき続ける作業は非常に億劫なのでできるだけ少ない回数で済ませたい時、あなたならどうする？

　試しに10問くらい考えてみましょう。暗算でもいいので自分が計算する様を思い描いてください。もちろん実際に電卓を叩いてもらっても構いません。
　　問1：2~5  　問2：3~12　問3：1~20　問4：13~14　問5：13~15
　　問6：7~16　問7：13~17  問8：2~5     問9：15~16　問10：13~16

何回くらい「＋」の記号を押したでしょうか。コツコツ真面目に毎回計算すると60回くらい押しているはずです。完全にランダムに問題が与えられるとして、平均5.0回は押さないといけない期待値計算になるので、大体100問で500回くらい押すことになりそうです。

　これはさすがにうんざり。例えば、問1と問8は同じ問題なので、問1の計算後に答えをメモっておけば問8での計算は全く不要。もっと言えば、A,Bの組み合わせは136通りしかないので、先に136通り求めておけば後は答えるだけ！じゃあ136通り求めるのに何回くらい「＋」を押すかというと、例えば1～4の計算結果に番号5の値を足せば1～5の結果になるので、「1から始めた場合」「2から始めた場合」・・・「15から始めた場合」で合計 15+14+・・・＋1 = 120回。これだけ押せば、たとえ1000問出題されてもビタイチ追加で押す必要はありません。真面目に毎回計算する１／５で済みました。

　さて、では次の場合は・・・

160個の数値と、それぞれに振られた番号が前問のように与えられています。また、あなたの手元には電卓とメモ帳があります。
これから100問あなたに質問します。（以下同文）

 　同じように計算すると、真面目にやると期待値で5300回。全通り計算する方法では12720回。組み合わせが増えてきて全通りの方が厳しそうになってきました。

　毎回真面目に計算するのと、あらかじめ全部計算するのと、それらの間にもっといい方法がないだろうか。ある程度質問ごとに計算するんだが、1回の計算は事前に計算したメモを参照して簡略化できるような・・・？

　で、例えばこういうのがあります。累積和。

　　　　　　　　　　　　　　　（図は16個の場合）

　最初の例で説明した、1から始めた場合の答えだけ覚えておく。すると、例えば5～9の和を聞かれた場合は、1～9の和（116)から1～4の和（50）を引けば66と答えられます。

　先の160個の場合、この方法だと、下準備に159回、各質問に1回の計算×100問でなんと259回の計算で済みます！！1ケタ以上少ないですね、楽ちん！

　とまあ、こんな感じで、うまくアルゴリズムと覚えておくデータの持ち方を考えて、限られたリソースと時間の中で問題を解くというのが競技プログラミングでよく問われる問題です。どうでしょう、楽しそうでしょうか？物足りない？ではこんな意地悪が入ります。

160個の数値と、それぞれに振られた番号が前問の様に与えられています。また、あなたの手元には電卓とメモ帳があります。
これから100問あなたに質問します。1問の質問は簡単で以下の要領です。

• 2つの番号 A,B (但しA ≦ B)をこちらが指定します。番号Aから番号Bまでに対応する数値の総和を答えなさい
• 但し、私は気まぐれなので、2～3問に1回、ランダムに１つ選んだ番号の値を書き換えます。どこを何に書き換えたかは教えます。 

 　こんなことをされると、せっかく作った累積和メモを変更のたびに毎回更新しないといけないので大変。。。

「もう、無理じゃね？」

　大丈夫、セグメント木ならね。

　　　　　　　　　　　　　　　（図は16個の場合）

　トーナメント式に計算した値を保持しておくと、少し1回の計算数は増えるが、任意の組み合わせについて16個の場合で高々4回、160個でも高々8回の計算で質問に答えることができます（下図の要領）

さて、累積和より少し計算数が増えたこの構造、メモの更新という新たな問題に対して素晴らしい効果を発揮します。具体的には下の図を見てもらえば雰囲気が分かるかと思います。

　累積和だと、変更された箇所より先は全て影響を受けるので、それらすべてを再計算しないといけないのですが、セグメント木は上方向の値を更新するだけです（これでうまくいく理由はトーナメントの感覚的にわかると思います）。

　このような感じで、与えられた問題に対してどうやるのが最適か？というアルゴリズム的な部分、それをプログラムでどう表現するかというプログラミングの部分。それを適切に選び、時間内にプログラムを書き提出する。とても競技要素の高い知的ゲームが競技プログラミングです。登るべき山は高くまた裾野は広いため、長く楽しめるものだと思います。
（chokudaiさんのアルゴリズム擬人化の話で似たようなことを話されていますが、個人的には格ゲーに似た感覚があると思っています。どのキャラがどういう技を持っていてどういう局面に強いのか、みたいな。あと「強い人はフレームが分かる」とか「コマンド入力が恐ろしく無駄がなく正確」とかそういうとこも）

仕事の役に立つの？

（ここはいわゆるチラ裏なので、興味のない方は次のセクションへ）

 個人の感想であり、効果には個人差があります。自分の場合はほとんど日々の業務には直結しないです。ただ、業務に直結しない＝役に立たないと断じてしまうのは早計だとは思います。以下は私見というか単なる僕個人の思い込みですが、例えばこういう利点があると思います。

• エンジニア寿命という考え方
  　ドラッガーの引用で恐縮ですが、「知識労働者の寿命はもはや企業の寿命より長い」という考え方があります。エンジニアは知識労働者です。企業寿命というと大げさに響くかもしれませんが、プロジェクトと言い換えると、自分の携わるプロジェクトが2,3年で変わってしまうことなどは割とありふれている事だということは想像に難くないと思います。すると、当座の業務に直結することが第一の正義という主張は必ずしも肯定されるものではありません。経験上、それよりもある程度のスキルと思考力で手を動かせることの方が、環境適応という点で大切な局面が多いように思います。ちょっとしたプログラムの読み書きでデータの挙動を眺めてみる、その一手が打てるか打てないかは大きいため、プログラムが書けることはそのまま財産になります。競技プログラミングでプログラミング能力は間違いなくある水準までは高まるため、エンジニア寿命にとって有益といっても良いと考えます。（と、１０年前の自分に教えてあげたい）
• 競技プログラマ達のコミュニティの中に身を置くという事
  　語弊を恐れずに言えば、それなりに真面目に10年ほど働くと、「この件に関して自分が一番詳しい」という局面がちょくちょく出てきます。それは良いことでもあるのですが、増えすぎると自分の能力律速になってしまい、気づかないうちに飽和してしまうという事もあります。その点において、競技プログラミングの世界には、もう訳分からんくらい頭のキレる人が山のようにいます。中学生にフルボッコにされたりします。まぁ大学の時もそういう人々に囲まれた生活だったので、懐古的と言えばそういう気持ちもないでもないです。
• Tシャツとかもらえるらしい
  　僕はもらったことないです。2014年という年は特に学生の競技プログラマを取り巻く環境にとっての大きな変化の年だったようで、CodeFestivalはじめさまざまな意欲的な取り組みがあちこちで催されていました。Ｔシャツだけじゃなく焼肉がついてくるらしい？社会人競技プログラマからすれば羨ましい限りという思いを抱かれた方も少なからず居るかと勝手に妄想してますが、大体よく言われているように技術者の職場マッチングはこれからもまだまだなくなることのない課題だと考えれば、今の世代の学生さん達が社会人となって3年目くらいとか、5年目くらいとか、まだまだ社会人ワンチャンみたいなイベントは増えるかも（もっともその頃には僕はもう中堅より上の年齢層で、やはり人権はないかもですが、労働サイクル自体が伸びている可能性もあるし、うーんなかなか）。あとやっぱりGCJシャツとかゲット出来たらちょっとかっこいい。
• レーティング
  　大体のコンテストサイトには独自のレーティング制度があります。コンテスト成績の良し悪しに応じてそのプレイヤーのランクが数値化されていて、上位の数%の人たちは神か悪魔かといったふうな扱いです。こういうレーティング制度みたいなものも賛否両論ありますが、個人的には自身の能力を量る指標としてはいいものだと思います(よく言われるのに「レーティングの数値≠実際の能力」だから意味がない、害悪だ、ということがありますが、それは精度の問題であってレーティングすることの問題ではない）。精度が多少犠牲になっていても、実際レーティングが上がればやる気は向上するし、下がれば悔しい思いをする。そういう競争的な刺激のあるものは、仕事の上ではあまり無いから余計そう感じているのかも(成果主義とか、評価関数を成果でしか測れないと諦めたところから生まれた言葉だと思っている)。

 まあ、何でもそうなんですが、あくまで競技プログラミングを練習することで得られる最大の効果は競技プログラミング能力の向上であって、仕事に役に立つとかいうのは運が良ければ副次的に得られるものです。本筋ではない部分にまで直截的な効果ばかりを求めるのは近道なようでいてあまり身にならないことが多い（と個人的には思っている）ので、あくまで種を蒔くというスタンスが自分には合っていて、上に書いたようにTシャツ目指すとか、レーティングに一喜一憂するとか、いろんなタイプのかしこい人の考え方に触れるとか、そういうちょっとしたことが大切だなと思います。

もしこんな感じで、そろそろ仕事にも慣れてきたなと感じている方は、ちょっとした頭の体操がしたい、新しい言語を練習したい、自分のスキルがどんなものか試したい、などなどそれくらいの軽い気持ちが湧いたなら、これを期に始めてみるのもいいのではないでしょうか（ここでタイトルノルマクリア）。

あと箇条書きで僕にとっての良かった／悪かった点を挙げるとすると、

• （良い点）C#覚えた。（OOPもついてきたのでこれは大きいな）
• （悪い点）C#がベターＣみたいになっとる。
• （良い点）twitterを始めた　（プロコン勢はtwitter率たかい）
• （悪い点）twitterを始めてしまった
• （良い点）コーディング速度が上がった
• （悪い点）仕事でのコーディング量は減った（昔は、自動化できるものは割と嬉々としてマクロ化したりしてたが、最近はプログラムにはプログラムにしかできないことをやらせたくなって、人の手でできることをマクロ化したりする事の魅力が減ってきた。これはまずい）
• （良い点）趣味の充実によるリフレッシュ（仕事自体は今年はクソ忙しかったんだよなぁ・・・）
• （悪い点）趣味の充実によるインドアライフの加速

君、これではトータルでマイナスではないかね？いやいやそんなことは。

蛇足ついでに、twitterを見ているとこの話題は「月刊競技プログラミングは役に立たない」などという定期スレが立つ話題のようですが、こういう「○○が何の役に立つのか」というテーマは僕自身理学部数学科の出身ということもあって、就活していたころのことを思い出してなんか懐かしくなります。折しも当時は大学の独立行政法人化の波などがあり、虚学だどうだと槍玉にあがることもあったのでいろいろ考えたものですが、10年働いた今思うことは2つ。

• （仕事がイケイケの時）「誰だよ数学なんか役に立たないって言った奴は！（以下某こくじんさんの名セリフを適宜置き換え」
• （仕事がダメダメの時）役に立たないのは数学じゃなくて僕のほうorz

競プロと数学と共通して言えるのは、正解に向かって正しく思考できている時には、それが正しいと感覚的に分かるというところで（いわゆる筋というやつ）、数学とほぼ関係ない今の仕事にあっても、筋の良し悪しが判別できるようになってきたころからうまく回せるようになってきたと思うので、そういうところを習得できることは大事だと思ったり。ただそれが数学や競プロでしか養えないか・最適か、となるとそれはまた別。

どんなコンテストがあるの？

　いろいろあります。僕が参加したものはおおむね冒頭で挙げてしまってますが、以下にコメントとリンクなどまとめてみました（今回の記事テーマを機能的にフォロー）

コンテスト形式	コンテスト名	開催頻度	出題形式	コメント
コンテスト系	AtCoder	毎週～隔週・ほぼ土曜固定	ARC　4問／90分	日本語なのでとっつきやすい。コンテスト後の解説放送が確実に競プロ界の底上げを加速している。後半2問は難しめ。
			ABC　4問／120分	「初心者向け内容」で2完とかで凹む事も。あと1問目10秒サブミットとか意味が分かりません。
	TopCoder	隔週弱くらい、曜日不定	SRM　3問／75分＋15分	div1とdiv2がある。定期コンテストとしては一番有名どころなのかな。英語だが読み易いのでそれほど気にならない。
	codeforces	隔週強くらい、曜日不定	5問／120分	div1とdiv2がある。毎回4-5000人くらいエントリーしていてビビる。その多さからサーバーがよく不安定になる。そこからサイトが不安定なことを「こどふぉる」また、英文が難解な問題が稀によくあり、「ReadForces」などと呼ばれる。
	yukicoder	火・木・日 23:20-	2問（！）1時間後くらいから解説	yuki2006さん個人運営のコンテストサイト。最近勢力拡大中。すごい。
	HackerRank	隔週弱くらい、曜日不定	いろいろ	weeklyChallengeや、48時間コンテストなど、社会人には一見嬉しいサイズのコンテストがあって個人的には結構好き。
	HackerEarth	いろいろ？	いろいろ	AC取ると「よくできました！」、WAとると「頑張れ頑張れできるできる絶対出来る頑張れもっとやれるって！」みたいなメールが来る。
オンラインジャッジ系	AOJ	いつでも	ICPC等の過去問が充実	日本語でとっかかり易く、問題も簡単なものからタフなものまであるので、いきなりコンテストはちょっと、という方はこれで雰囲気に慣れるのがいいのかなと思います。
	ProjectEuler	いつでも	数学っぽい問題、1問必答	最初50問は数学ゲーというより全検索ゲーなので暇つぶしに。後半は見るからに難しそうな感じがしますがまだまだそこまで手をつけれてません。
その他	codeiq	出題が期間限定（～2,3週くらい）	回答に出題者からフィードバック。	難易度はそれほど高くない問題が多いが、いろんな方が出題されていて面白い。ゴルファーやマルチリンガルプログラマがうろうろしていて怖い

ちなみに僕のレーティングはSRMが1214、Codeforcesが1720とともに1年かけてようやくdiv1に滑り込んだくらいです。自分的にはまぁまぁこんなもんか、ちょっとよくできた方かなと思ってます。来年はdiv1安定から黄色ワンチャンくらいを目標に。あとなんでもいいからTシャツ欲しい。

まとめ

何事も始めるのに遅すぎるという事はないし、なにより「今まで知らなかった知識が増える」「これまでできなかったことが出来るようになる」これらの快楽は中毒性が半端ないので、興味湧いた方は是非やってみましょう！スタートコストが低いのもエコでお勧めですよ！